
如今,人工智能 (AI) 的突破越来越频繁地成为新闻头条。至少就目前而言,人工智能是深度学习的代名词,这意味着基于神经网络的机器学习(如果你不知道神经网络是什么,不要担心——在这篇文章中你不需要它们)。
深度学习的一个领域引起了很多兴趣,也有很多很酷的结果,那就是图神经网络(GNN,graph neural networks)。
这种技术使我们能够喂送自然存在于图上的神经网络数据,而不是像欧几里得空间这样的向量空间。这种技术流行的一个重要原因是,我们现代以互联网为中心的生活大部分都发生在图(graph)中。
社交媒体平台将用户连接到海量图中,以账号作为顶点,友谊作为边(关注另一个用户,就对应于有向图中的一条有向边),而像谷歌这样的搜索引擎将网络视为有向图,网页作为顶点,超链接作为边。
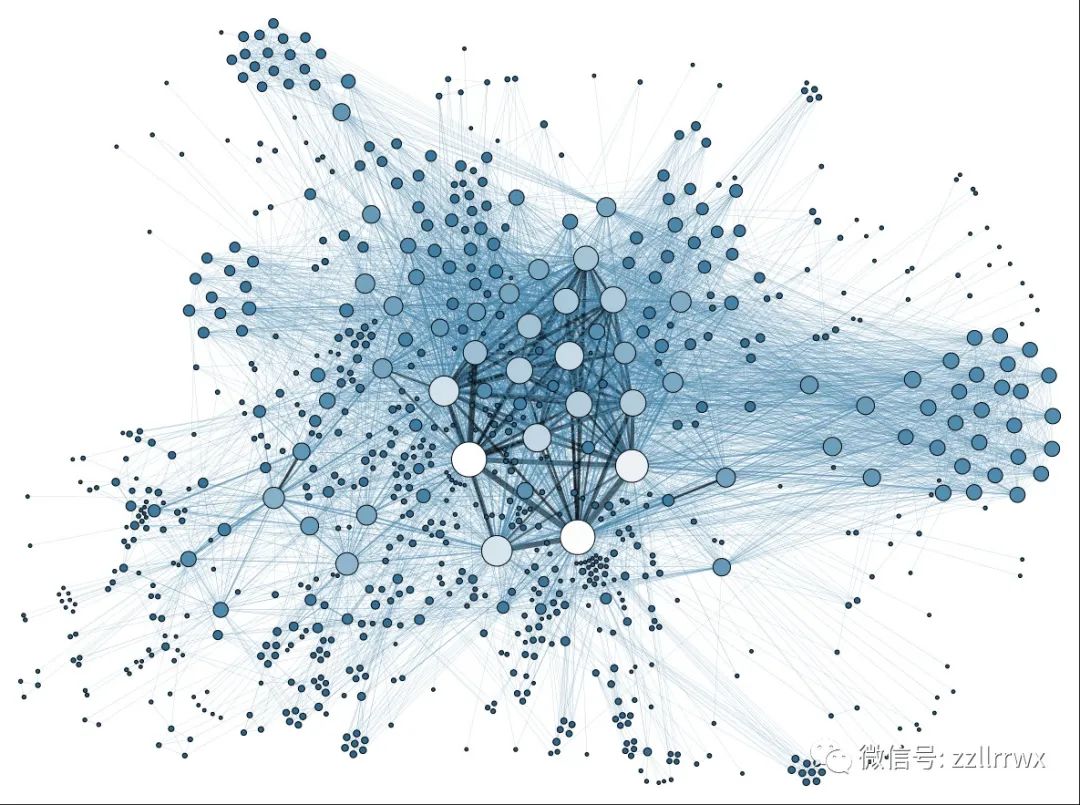
这是一个显示参与国际联盟的人员之间联系的图。图片来源:Martin Grandjean(CC BY-SA 3.0)
AirBnB提供了另一个有趣的示例。2021 年初,AirBnB 的首席技术官预测 GNN 将很快成为该公司的大生意。
事实上就在几个月前,AirBnB 的一位工程师在一篇博客文章中解释了他们现在使用 GNN 的一些方式以及这样做的原因。
这位工程师以下面鸟瞰方式开始了他的文章,说明为什么图对现代数据很重要——我将在这里引用,因为它完美地为我们奠定了基础:
许多现实世界的机器学习问题都可以被框定为图问题。在在线平台上,用户经常共享资产(例如照片)并相互互动(例如消息、预订、评论)。
用户之间的这些连接自然形成可用于创建图的边。但是,在许多情况下,机器学习从业者在构建机器学习模型时不会利用这些连接,而是将节点(在本例中为用户)视为完全独立的实体。
虽然这确实简化了事情,但忽略节点连接周围的信息可能会忽略该节点在整个图的上下文中的位置,从而降低模型性能。
在本专栏中,我们将探讨如何将每个节点缺失的图“上下文”硬塞回适合标准机器学习和统计分析的简单欧几里得格式。
这是一种更传统的处理图数据的方法,早于 GNN。基本思想是制作各种指标,将图的离散几何形状转换为附加到每个顶点的数字。
这是一个有趣的设置,可以看到一些图论的实际应用,你不需要事先知道任何机器学习——我会从快速温和地回顾你需要的一切开始探讨。
机器学习中的三个主要任务是回归(regression)、分类(classification)和聚类(clustering)。
对于回归,你有一个称为特征的变量集合和一个附加变量,必须是数值(实数值,在ℝ中) 称为目标变量;
通过考虑特征和目标值都已知的训练数据,你可以拟合一个模型,该模型尝试在已知特征但目标值未知的实际数据上预测目标值。
例如,根据大学生的 GPA 和他们就读的大学预测大学生毕业后的收入是一项回归任务。
假设所有特征都是数字的——例如,我们可以用每所大学的《美国新闻》排名来表示(暂时忽略这些排名的一些问题)。
然后一种常见的方法是线性回归,即当你在欧几里得空间中找到一个超平面,由特征和最适合训练数据的目标值的坐标(即,最小化从训练点到超平面的“垂直”距离)。
分类,非常相似;唯一的区别是目标变量是分类变量而不是数值变量——这在数学术语中只是意味着它在有限集合中取值,而不是在ℝ中。
当此目标集的大小为 2 时(通常{真,假}{Tru e,False}或{是,否}{yes,no}或{0,1}{0,1}) 这称为二元分类。例如,预测哪些学生将在毕业后一年内就业可以框定为二元分类任务。
聚类,略有不同,因为没有目标,只有特征,并且你希望根据这些特征以某种自然的方式将数据划分为少量子集。
这里没有正确或错误的答案 - 聚类往往更像是一种探索性活动。
例如,你可以尝试根据大学生的 GPA、SAT 分数、经济援助金额、参加的荣誉课程数量和参加的校内运动数量对大学生进行聚类,然后查看聚类是否具有人类可解释的描述,这可能有助于理解学生如何划分队列。
我想为你提供一种回归和分类方法的详细信息,以便在我们转向图时为你提供一些具体的想法。让我们做 k -最近邻 (k-NN,k-Nearest Neighbors) 算法。
这个算法有点好笑,因为它实际上并没有将模型与通常意义上的训练数据拟合——为了预测每个新数据点的目标变量值,算法直接回顾训练数据并基于它进行计算。
从修复整数开始 k≥1K≥1(较小的 k 值提供本地化的精细数据视图,而较大的值提供平滑的聚合视图)。
给定一个具有已知特征值但目标值未知的数据点P,该算法首先找到k个最近的训练点Q1,...,QkQ1,...,Qk——其中训练点Qi特征值在欧几里得空间中到 P 的距离最小。
然后,如果任务是回归的,则 P 的预测目标值是Q1,...,QkQ1,而如果任务是分类,那么这些类别
Qi问一被视为投票和预测P点的类,P是获得最多选票的分类。(不用说,有很多变体,例如按到P点距离加权平均值/投票,将平均值更改为中位数,或将度量从欧几里得更改为其他东西。)
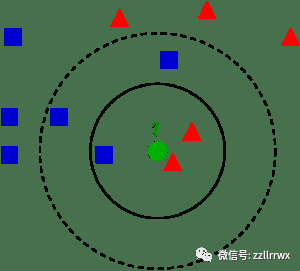
一个绿色点及其3-最近邻和5-最近邻。图片来源:Antti Ajanki(CC BY-SA 2.5)
这就是你需要了解的有ℝⁿ中数据点所在的通常欧几里得环境中的机器学习的全部信息。
在转向存在于图中的数据点之前,我们需要讨论一些图论。
如果图形中的两个顶点通过边连接,则它们是相邻点(neighbors,邻居)。
如果两条边具有共同的顶点,则它们是相邻边(adjacent edges)。
两个顶点之间的距离(distance)是它们之间最短路径的长度,其中这里的长度仅表示路径中的边数。
要记住的一个有用例子是像Facebook这样的社交媒体平台,其中顶点代表用户,边代表他们之间的“友谊”。
(这是一个无向图;像Twitter和Instagram这样的平台,其中账号相互不对称地跟随,形成了有向图。)
本文中的所有内容都可以通过微小的修改来完成有向图,但为了简单起见,我将坚持使用无向情况。
在这个例子中,你的邻居是你的 Facebook 好友,如果你们不是好友,但有一个共同的朋友,则他与距离是 2。
以你为中心的半径为 6 的闭合球(即距离你最多 6 个距离的所有账号)由你在平台上最多可以到达 6 度分隔的所有 Facebook 用户组成。
接下来,我们需要一些方法来量化顶点在图中扮演的结构角色。这一堆顶点中,有许多刻画了图的中心度的各种概念;我在这里只提供一些。
从最简单的开始,我们有顶点的度(degree),在没有循环或多条边的图中,度就是该顶点邻居的数量。
在Facebook中,你的度数就是你的朋友数量。(在有向图中,度数分为入度和出度的总和,在Twitter上,即计算关注你的用户数和你关注的用户数。
顶点的接近度(closeness )刻画它是位于图形中心附近还是外围。它被定义为图中此顶点与其他顶点之间的距离之和的倒数。
靠近中心的顶点与其他顶点的距离相对较小,而更外围的顶点到某些顶点的距离适中,但与图“相反”侧的顶点的距离很大。
这意味着中心顶点的距离总和小于外围顶点的距离总和;此总和的倒数会将其翻转过来,以便中心顶点的接近度得分大于外围顶点。
粗略地说,顶点的中介度(betweenness )根据图中通过顶点的路径数量来刻画中心度。
更准确地说,它是图中所有其他顶点对的总和,即通过相关顶点的一对顶点之间的最短路径的比例。
这很拗口,所以让我们用几个简单的例子来拆解它。请考虑以下两个图:
(a)![图片]() (b)
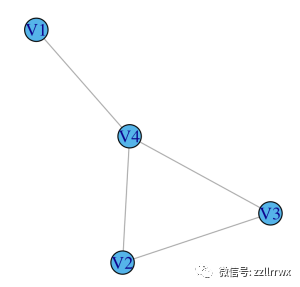
(b)![图片]() 在图 (a) 中,V1 的中介度为 0,因为其余顶点之间没有最短路径通过 V1。V2 和 V3 也是如此。
然而,V4 的中介度为 2:在 V1 和 V2 之间有一条唯一的最短路径,它通过 V4,同样,在 V1 和 V3 之间有一条唯一的最短路径,它也通过 V4。
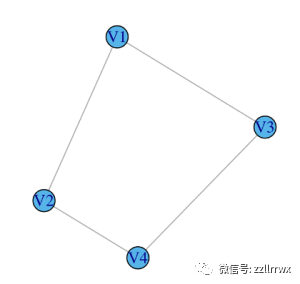
对于(b)中的图,通过对称性,足以计算单个顶点的中介度。V1 的中介度为 0.5,因为在 V2 和 V3 之间有 2 条最短路径,其中正好有一条通过 V1。
其中 (a) 每个顶点的大小对应于其接近度分数,在 (b) 中对应于中介度分数。
中介度更难直接解释,但粗略地说,它有助于识别图中的重要桥梁。
(a)
在图 (a) 中,V1 的中介度为 0,因为其余顶点之间没有最短路径通过 V1。V2 和 V3 也是如此。
然而,V4 的中介度为 2:在 V1 和 V2 之间有一条唯一的最短路径,它通过 V4,同样,在 V1 和 V3 之间有一条唯一的最短路径,它也通过 V4。
对于(b)中的图,通过对称性,足以计算单个顶点的中介度。V1 的中介度为 0.5,因为在 V2 和 V3 之间有 2 条最短路径,其中正好有一条通过 V1。
其中 (a) 每个顶点的大小对应于其接近度分数,在 (b) 中对应于中介度分数。
中介度更难直接解释,但粗略地说,它有助于识别图中的重要桥梁。
(a)![图片]() (b)
(b)![图片]() 图中顶点重要性/中心度的另一对有用度量是特征向量中心度得分和PageRank得分。
它们在与邻接矩阵相关的特征向量和图上的随机游走方面都有很好的解释。
假设我们有用于机器学习的通常形式的数据——即用于聚类的特征,或者如果你正在做回归/分类,那么还有一个目标变量——但除此之外,假设数据点形成了图的顶点。
合并这种图结构的一种简单但非常有效的方法(即,不要忽略每个顶点“在整个图的上下文中”的位置,用AirBnB工程师的话来说)是简单地附加前面讨论的顶点指标给出的一些附加特征:度数,接近度,中介度,特征向量中心度,PageRank(除此之外还有很多其他特征)。
例如,可以以这种方式执行聚类,这将基于顶点的图论属性以及原始的非图论特征值对顶点进行聚类。
具体来说,如果将接近度作为单个附加的图论特征添加,则生成的聚类更有可能将外围顶点放在相同的聚类中,并且更有可能将图中心附近的顶点放在相同的聚类中。
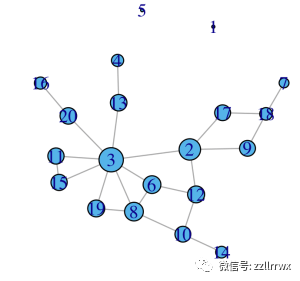
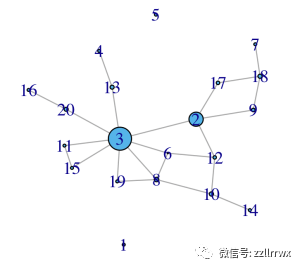
下图显示了前面所示的相同的 20 顶点随机图,现在的顶点由聚类算法着色(k 均值,对于k=3),它使用两个图论特征:接近度和中介度。
我们得到一个包含两个孤立顶点的簇,一个簇包括两个非常中心的顶点,一个簇包含其他所有内容。
如果预测大学生毕业后的起始收入,则可以使用具有上述传统特征的回归方法,但包括其他特征,例如每个学生在网络中的特征向量中心度,这些特征由连接学生形成的网络,只要他们一起上一节课。
图中顶点重要性/中心度的另一对有用度量是特征向量中心度得分和PageRank得分。
它们在与邻接矩阵相关的特征向量和图上的随机游走方面都有很好的解释。
假设我们有用于机器学习的通常形式的数据——即用于聚类的特征,或者如果你正在做回归/分类,那么还有一个目标变量——但除此之外,假设数据点形成了图的顶点。
合并这种图结构的一种简单但非常有效的方法(即,不要忽略每个顶点“在整个图的上下文中”的位置,用AirBnB工程师的话来说)是简单地附加前面讨论的顶点指标给出的一些附加特征:度数,接近度,中介度,特征向量中心度,PageRank(除此之外还有很多其他特征)。
例如,可以以这种方式执行聚类,这将基于顶点的图论属性以及原始的非图论特征值对顶点进行聚类。
具体来说,如果将接近度作为单个附加的图论特征添加,则生成的聚类更有可能将外围顶点放在相同的聚类中,并且更有可能将图中心附近的顶点放在相同的聚类中。
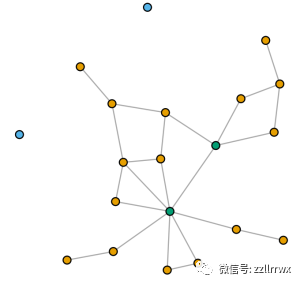
下图显示了前面所示的相同的 20 顶点随机图,现在的顶点由聚类算法着色(k 均值,对于k=3),它使用两个图论特征:接近度和中介度。
我们得到一个包含两个孤立顶点的簇,一个簇包括两个非常中心的顶点,一个簇包含其他所有内容。
如果预测大学生毕业后的起始收入,则可以使用具有上述传统特征的回归方法,但包括其他特征,例如每个学生在网络中的特征向量中心度,这些特征由连接学生形成的网络,只要他们一起上一节课。
到目前为止,我们已经通过结合图论特征来增强传统的机器学习任务。我们的最后一个主题是传统的非图论世界中没有对应项的机器学习任务:边预测。
给定一个图(可能具有每个顶点的特征值集合),我们想预测哪条边最有可能形成下一条,当图形被认为是一个动态过程时,其中顶点集保持不变,但边随着时间的推移而形成。
在Facebook的背景下,这是预测哪两个还不是Facebook好友的用户最有可能成为朋友,一旦Facebook做出这个预测,它就可以将其用作建议。
我们不知道Facebook实际使用的方法(我的猜测是它至少涉及GNN),但我可以解释一种在数据科学社区广泛使用的非常自然的方法。
我们首先需要机器学习的额外背景成分。大多数分类器不是直接预测数据点的类别,而是首先计算倾向(propensity)分数,直到归一化,这基本上是每个分类的估计概率,然后预测的分类是倾向得分最高的类。
例如,在 k-NN 中,我说预测是通过计算每个类中的邻居数量并取最普遍的类来给出的;这些类计数是 k-NN 分类的倾向分数。
具体来说,对于 10-NN,如果一个数据点有 5 个红色邻居、3 个绿色邻居和 2 个蓝色邻居,那么红色的倾向得分为 0.5,绿色的倾向得分为 0.3,蓝色的倾向得分为 0.2(当然,预测本身是红色的)。
对于二元分类,通常只报告0到1之间的单个倾向分数,因为另一个类的倾向得分只是互补概率。
回到边预测任务,考虑一个有 n 个顶点的图,想象一个从 n 个中选择 2 行的矩阵,由图中的顶点对索引。
此矩阵的列是与顶点对相关的特征 - 可以是类似于一个顶点对中的两个顶点的接近度(或中介度,或特征向量中心度,或...)得分的平均值(或最小值或最大值),如果存在与顶点关联的非图论特征,也可以从中得出, 也可以使用这两个顶点之间的距离作为特征。
创建一个附加列,扮演目标变量的角色,如果顶点对是邻居(即有一条边连接),则为 1,否则为 0。
在此数据上训练二元分类器,在非邻居中倾向得分最高的顶点对是最倾向于成为邻居的对 - 也就是说,根据所使用的特征,这是最有可能形成的下一个边。
基于图的结构(以及外在的非图数据,如果也使用它的话),这揭示了尚不存在的边。
如果有图随时间演变的快照,就可以在 t 时刻在图上训练这个二元分类器,t然后将预测的边与以后的时刻t′>tt′>t,存在的实际边进行比较,以了解这些边预测的准确性。
概括地说,这是我们在本文中采取的路径以及我们最终的位置。
图中顶点之间的距离——概括了凯文·培根(Kevin Bacon)的电影角色和保罗·厄尔多斯(Paul Erdős)合作的流行的“分离度”游戏——允许人们通过中介度和接近度等概念来量化顶点所扮演的各种图论角色。
然后,这些量化可以作为聚类、回归和分类任务的特征,这有助于所涉及的机器学习算法将图形结构整合到数据点上。
通过将顶点对视为数据点,并使用每对的平均接近度、中介度等(和/或对之间的距离),我们可以预测图中“应该”存在哪些缺失的边。
当图是社交媒体网络时,这些缺失的边可以框定为算法的朋友/关注者建议。
当图是数学合作时(数学家作为顶点和边连接共同撰写论文的对),这可以告诉你你的下一个合作者应该是谁:只要找到那个倾向得分最高的你还没有和他一起发表的数学家!
延伸阅读
-
对于我们每天依赖的社交媒体和搜索网络以及其中涉及的机器学习算法的非技术性讨论,可以尝试我的书《算法如何创建和防止假新闻》。
-
对于大数据和预测算法伦理的非技术性讨论,Cathy O'Neil的《数学毁灭武器》
-
对于网络和网络科学的教科书,Albert-László Barabási的《网络科学》
-
对于将机器学习应用于网络数据的教科书,Aggarwal和Murty的《社交网络中的机器学习》
https://mathvoices.ams.org/featurecolumn/2022/10/01/predicting-friendships-and-other-fun-machine-learning-tasks-with-graphs/


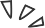
文章评论