非线性关系解决异或问题
本文讲解了使用非线性神经网络解决异或问题,谈及了参数初始化的方式,分类问题中使用crossEntropy而不用MSE的原因。
一、正常解决异或关系方法
import numpy as np
import matplotlib.pyplot as plt
x_data = np.array([[1,0,0],
[1,0,1],
[1,1,0],
[1,1,1]])
y_data = np.array([[0],
[1],
[1],
[0]])
# 初始化权值,取值范围为-1~1
v = (np.random.random([3,4])-0.5)*2
w = (np.random.random([4,1])-0.5)*2
lr = 0.11
def sigmoid(x):
return 1/(1+np.exp(-x))
def d_sigmoid(x):
return x*(1-x)
def update():
global x_data,y_data,w,v,lr,L1,L2,L2_new
L1 = sigmoid(np.dot(x_data,v)) #隐含层的输出4*4矩阵
L2 = sigmoid(np.dot(L1,w)) #输出层的实际输出4*1
# 计算输出层和隐含层的误差,然后求取更新量
#
L2_delta = (L2-y_data) # y_data 4*1 矩阵
L1_delta = L2_delta.dot(w.T)*d_sigmoid(L1)
# 更新输入层到隐含层的权值和隐含层到输出层的权值
w_c = lr*L1.T.dot(L2_delta)
v_c = lr*x_data.T.dot(L1_delta)
w = w-w_c
v = v-v_c
L2_new = softmax(L2)
def cross_entropy_error(y, t):
return -np.sum(t * np.log(y)+(1-t)*np.log(1-y))
def softmax(x):
exp_x = np.exp(x)
sum_exp_x = np.sum(exp_x)
y = exp_x/sum_exp_x
return y
if __name__=='__main__':
for i in range(1000):
update() #更新权值\
if i%10==0:
plt.scatter(i,np.mean(cross_entropy_error(L2_new,y_data)))
plt.title('error curve')
plt.xlabel('iteration')
plt.ylabel('error')
plt.show()
print(L2)
print(cross_entropy_error(L2_new,y_data))
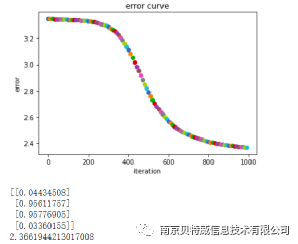
先来讲讲输入的数据x:第一列是偏置项恒置为1,后两列分别为x1,x2。而y是x1,x2对应的输出,即异或关系结果的标签。lr是设置的学习率。通过交叉熵计算损失。最终得出图下方的预测结果,不难看出预测结果还是十分接近标签的。
二、使用线性关系解决异或问题
import numpy as np
import matplotlib.pyplot as plt
x_data = np.array([[1,0,0],
[1,0,1],
[1,1,0],
[1,1,1]])
y_data = np.array([[0],
[1],
[1],
[0]])
# 初始化权值,取值范围为-1~1
v = (np.random.random([3,4])-0.5)*2
w = (np.random.random([4,1])-0.5)*2
lr = 0.11
def update():
global x_data,y_data,w,v,lr,L1,L2,L2_new
L1 = np.dot(x_data,v) #隐含层的输出4*4矩阵
L2 = np.dot(L1,w) #输出层的实际输出4*1
# 计算输出层和隐含层的误差,然后求取更新量
#
L2_delta = (L2-y_data) # y_data 4*1 矩阵
L1_delta = L2_delta.dot(w.T)
# 更新输入层到隐含层的权值和隐含层到输出层的权值
w_c = lr*L1.T.dot(L2_delta)
v_c = lr*x_data.T.dot(L1_delta)
w = w-w_c
v = v-v_c
L2_new = softmax(L2)
def cross_entropy_error(y, t):
return -np.sum(t * np.log(y)+(1-t)*np.log(1-y))
def softmax(x):
exp_x = np.exp(x)
sum_exp_x = np.sum(exp_x)
y = exp_x/sum_exp_x
return y
if __name__=='__main__':
for i in range(300):
update() #更新权值
if i%10==0:
plt.scatter(i,np.mean(cross_entropy_error(L2_new,y_data)))
plt.title('error curve')
plt.xlabel('iteration')
plt.ylabel('error')
plt.show()
print(L2)
print("最终误差大小为:",cross_entropy_error(L2_new,y_data))
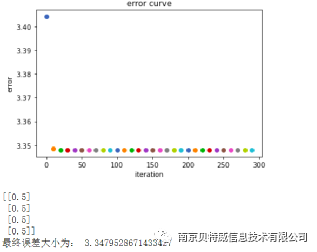
三、使用MSE作为损失函数解决异或问题
import numpy as np
import matplotlib.pyplot as plt
x_data = np.array([[1,0,0],
[1,0,1],
[1,1,0],
[1,1,1]])
y_data = np.array([[0],
[1],
[1],
[0]])
# 初始化权值,取值范围为-1~1
v = (np.random.random([3,4])-0.5)*2
w = (np.random.random([4,1])-0.5)*2
lr = 0.11
def sigmoid(x):
return 1/(1+np.exp(-x))
def d_sigmoid(x):
return x*(1-x)
def update():
global x_data,y_data,w,v,lr,L1,L2,L2_new
L1 = sigmoid(np.dot(x_data,v)) #隐含层的输出4*4矩阵
L2 = sigmoid(np.dot(L1,w)) #输出层的实际输出4*1
#
L2_delta = (L2-y_data)*d_sigmoid(L2) # y_data 4*1 矩阵
L1_delta = L2_delta.dot(w.T)*d_sigmoid(L1)
# 更新输入层到隐含层的权值和隐含层到输出层的权值
w_c = lr*L1.T.dot(L2_delta)
v_c = lr*x_data.T.dot(L1_delta)
w = w-w_c
v = v-v_c
L2_new = softmax(L2)
def softmax(x):
exp_x = np.exp(x)
sum_exp_x = np.sum(exp_x)
y = exp_x/sum_exp_x
return y
if __name__=='__main__':
for i in range(1000):
update() #更新权值\
if i%10==0:
plt.scatter(i,np.mean((y_data-L2)**2)/2)
plt.title('error curve')
plt.xlabel('iteration')
plt.ylabel('error')
plt.show()
print(L2)
print(np.mean(((y_data-L2)**2)/2))
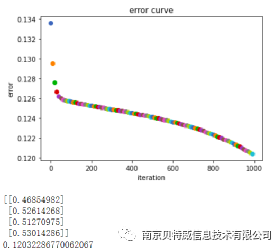
不难看出使用MSE也不能够解决异或问题,那么是什么原因呢?
从理论上将讲平方损失函数也可以用于分类问题,但不适合。首先,最小化平方损失函数本质上等同于在误差服从高斯分布的假设下的极大似然估计,然而大部分分类问题的误差并不服从高斯分布。而且在实际应用中,交叉熵在和Softmax激活函数的配合下,能够使得损失值越大导数越大,损失值越小导数越小,这就能加快学习速率。然而若使用平方损失函数,则损失越大导数反而越小,学习速率很慢。看下面这张图可以看出其中的问题。
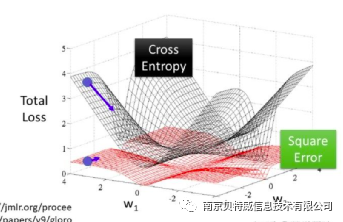
再看上面的第一张结果图和第三章结果图:



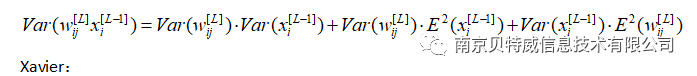
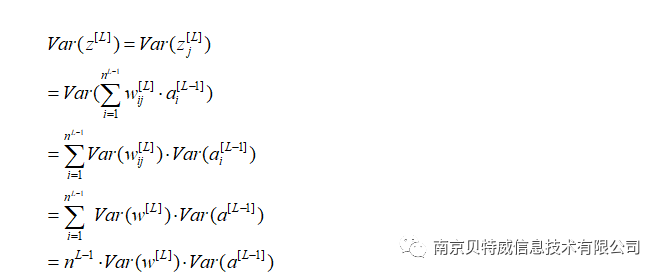
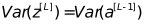
那么需要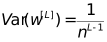
而在反向传播中,同理
需要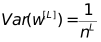
对于这两个数取调和平均数: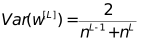
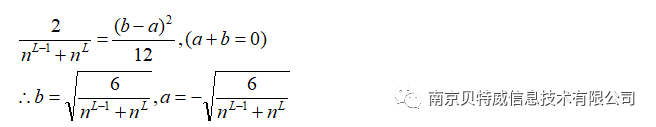
(a,b)即为初始化权重的范围。
本例中隐层神经元为4,所以可以近似将权重初始化范围设置为(-1,1)。
文章评论