独门绝技！打通python的第一道大关，你也可以！

2022年7月21日 330点热度 0人点赞 0条评论

哈咯大家好！高高低低，算法分析（单押!）

欢迎来到我们新一期的算法分析专题，我是低低。

大名鼎鼎的Numpy库，其实是一个能够实现科学计算的python模组。与其他不同的是，如果要存储数据，其储存在连续的内存块中，与其他的Python内置对象相独立。

同时。它其中使用C语言的算法库可以很轻松地对内存进行相应操作，没有其他的前期工作。NumPy数组所使用的内存与其他的内置序列相比更少。

而且，其它的Python 重量级的相关套件（如：Pandas、SciPy、Scikit-learn 等等）都几乎是奠基在 Numpy 的基础上。

所以，学会 Numpy才能为往后学习其他数据科学相关套件来分析影像组学打下坚实的基础呢！

（画外音：…….能不能说人话，我快要晕了）

别别别，不敢把大家绕弯。低低因为才疏学浅，还请感兴趣的捧油们移步前两年Numpy团队在Nature上发表的关于Numpy的新版介绍概述（doi: 10.1038/s41586-020-2649-2）。

（图片源自于Harris CR, Array programming with NumPy. Nature. 2020Sep;585(7825):357-362. ）

（画外音：蛤？那都是英文看不懂要怎么办？）

（低低：(ˉ▽ˉ；)… 好吧低低答应大家下次一定做一个单独的专题介绍这篇超高分综述！）

那下面我们就一起来初窥一下这个Numpy到底是何方神圣吧！

低低觉得，可以用一句话来总结Numpy的特点。

大家还记得我们上一期总结的口诀吗？

（画外音：（抢答）要想影像组学，先python!）

（低低：没错！）

那我们今天可以在这句后面加上两句话。

要想python，先Numpy。要想Numpy，先阵列！

所以从这句话中我们可以看到，Numpy中最经典的就是阵列操作。

（低低：所以可以说，如果你会阵列操作，基本上你就可以掌握Numpy啦！）

这就是Numpy阵列长的模样！

（画外音：哇，感觉比R的要好看很多耶( •̀ ω •́ )y）

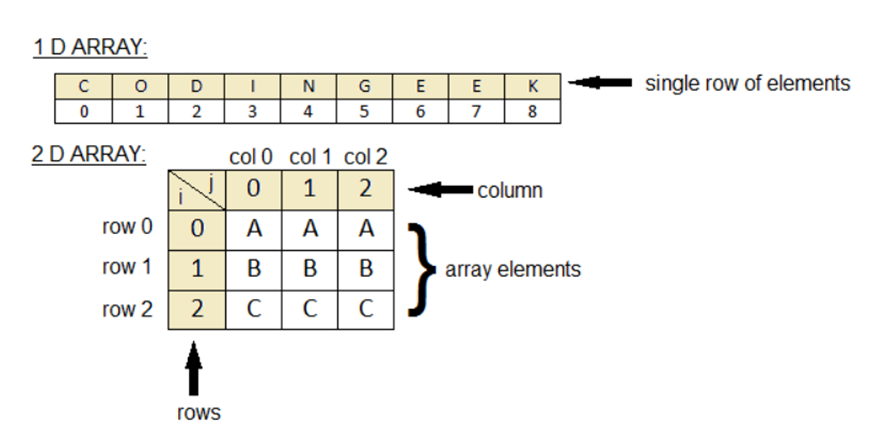
实际上，Numpy的所有功能都是建立在同质且多维度的 ndarray（N-dimensional array）上。

（低低：也就是类似电影《盗梦空间》里面的那样啦！）

ndarray 有几个关键属性，分别为维度（ndim）、形状（shape）和数值类型（dtype）。一般我们称一维数组为 vector 而二维数组为 matrix。

所以作为最开始的步骤，我们需要引入 numpy 模块，透过传入 list 到 numpy.array() 创建数组。

# 引入 numpy 模块

import numpy as np

np1 = np.array([1, 2, 3])

np2 = np.array([4, 5, 6])

那如果要加起来，怎么加呢？

（低低：直接加！（简单粗暴）

#阵列相加

print(np1 + np2)

# [5 7 8]

所以，我们可以通过以下操作来明确一个阵列的相关信息

#显示相关信息

print(np1.ndim, np1.shape, np1.dtype)

# 1 (3,) int64 => 一维数组, 三个元素, 数据型别

相信聪明的大家到这里都没有任何问题。

那么我们接下来再继续生成第三个阵列

np3 = np.array([1, 2, 3, 4, 5,6])

接下来，如果我们想要改变阵列的维度，比如从前面的一维变成二维

可以这么做

np3 = np3.reshape([2, 3])

print(np3.ndim, np3.shape, np3.dtype)

# 2 (2, 3) int64

大家一定注意到了吧，上面都会显示一个int64

那int64又是什么东西呢？

说到这个，我们就要来讨论一下阵列的型别，或者称为数据的类型。

常用的主要有以下四种bool、int、float、string。

bool 也就是我们高中学过的布尔，可以包含 True、False。

int 可以包含 int16、int32、int64。其中数字是指 bits。

float 可以包含 16、32、64 表示小数点后几位。

string 可以是 string、unicode。

而有时可能会出现nan ，则表示遗失值。

那接下来，我们来一个前面的汇总。

import numpy as np

a = np.arange(15).reshape(3, 5)

# array( [ [ 0, 1, 2, 3, 4],

[ 5, 6, 7, 8, 9],

[10, 11, 12, 13, 14] ] )

然后我们来逐个查看一下数据的内容。

print(a.shape)

print(a.ndim)

print(a.dtype.name)

print(a.itemsize) # bytes

print(a.size)

print(type(a))

输出的结果

(3, 5)

int64

大家都看明白了吧？

所以我们要掌握的第一步就是创建阵列，使用 np.array() 将Python list换为 numpy array。

a = np.array([2,3,4])

print(a)

print(a.dtype)

b = np.array([1.2, 3.5, 5.1])

print(b.dtype)

输出结果

[2 3 4]

int64

float64

除了人为的添加进去阵列的内容，我们当然也可以通过函数的方式添加

比如下面两个函数

np.arange()

np.linspace()

我们先来通过观察下面的结果看看两者的区别。

from numpy import pi

print(np.arange(10, 30, 5))

print(np.arange(0, 2, 0.3))

print(np.linspace(0, 2, 9))

出来的结果

[10 15 20 25]

[0. 0.3 0.6 0.9 1.2 1.5 1.8]

[0. 0.25 0.5 0.75 1. 1.25 1.5 1.75 2. ]

（画外音：咦？第三个怎么怪怪的）

事实上，两者的区别就在于

arange()类似于内置函数range()，通过指定开始值、终值和步长创建表示等差数列的一维数组，注意得到的结果数组不包含终值。

而linspace()通过指定开始值、终值和元素个数创建表示等差数列的一维数组，可以通过endpoint参数指定是否包含终值，默认值为True，即包含终值。

这就是两者的差别。

（画外音：哇！好神奇！还有其他函数嘛）

当然有！比如：

np.random.rand()

np.random.randn()

np.fromfunction()

np.fromfile()

这几个函数，就请大家自行探索一下啦！

同时阵列还能通过指定axis来查看各行各列的情况。

axis=0 表示各行的总称

axis=1 表示各列的总称

比如

b = np.arange(12).reshape(3,4)

print(b)

print(b.sum(axis=0))

print(b.min(axis=1))

print(b.cumsum(axis=1))

结果显然为

[ [ 0 1 2 3]

[ 4 5 6 7]

[ 8 9 10 11] ]

[12 15 18 21]

[0 4 8]

[ [ 0 1 3 6]

[ 4 9 15 22]

[ 8 17 27 38] ]

大家要注意喔，python的行列计数是从0开始的哟！

（画外音：哇，这么多种生成阵列的方式。那有没有拆分阵列呢？）

俗话说得好，分久必合，合久必分。有分就有合。这是万事万物的自然规律。

所以我们再来看看如何切割以及索引阵列。

a = np.arange(10)**3

print(a)

print(a[2])

print(a[2:5])

print(a[:6:2])

print(a[::-1])

得到的结果

[ 0 1 8 27 64 125 216 343 512 729]

[ 8 27 64]

[ 0 8 64]

[729 512 343 216 125 64 27 8 1 0]

大家看，第一行其实是制造10个从0开始的三次方的数字。

而我们print第2个数，显然是8。再接着，print第2到5个数字，得到8，27，64。

所以关键的要点就在于，一定要明白，python计数是从第0个开始的喔！

（画外音：amazing！）

再看看两个例子来实操一下

print(b[2, 3])

print(b[0:5, 1])

print(b[:, 1])

print(b[1:3, :])

可得到

[ 1 11 21 31 41]

[[10 11 12 13]

[20 21 22 23]]

def f(x, y):

return 10*x + y

b = np.fromfunction(f,(5,4),dtype=int)

print(b)

可得到

[ [ 0 1 2 3]

[10 11 12 13]

[20 21 22 23]

[30 31 32 33]

[40 41 42 43] ]

（画外音：感觉这个阵列真的很有趣，比R有意思多啦！）

既然今天掌握了Numpy的基本知识，那我们下一期就继续来看看Numpy运用在影像组学上有什么技巧吧！

请锁定下一期的高高低低专栏喔~

—END—

撰文丨吐吐

审核丨小糕老师

责编丨小张老师

往期推荐

515500独门绝技！打通python的第一道大关，你也可以！

独门绝技！打通python的第一道大关，你也可以！

文章评论