bootstrap方法如何应用在统计学和风险预测模型研究中

点击上方蓝字关注，更多统计、科研干货等你来挖掘哦~

月半小夜曲

一、什么是bootstrap？

Bootstrap一词源于西方神话故事中的一句话：to pull oneself up by one's bootstrap，译成中文就是：自己帮助自己。

bootstrap是统计学中一种十分常用的数据采样方式，其核心思想是：采用重复有放回方式对原始数据进行多次抽样。

划重点了，这句话有3层重要意思：

（1）抽样方式是有放回的：即A这次被抽中，下次还可能被抽中，因为每次抽到的样本还要放回抽样盒中；

（2）是等量抽样：即每一轮抽取的样本量和原数据集样本量相同；

（3）抽样重复多次：bootstrap一般要进行多轮，次数因人而异，如100、500、1000次等。

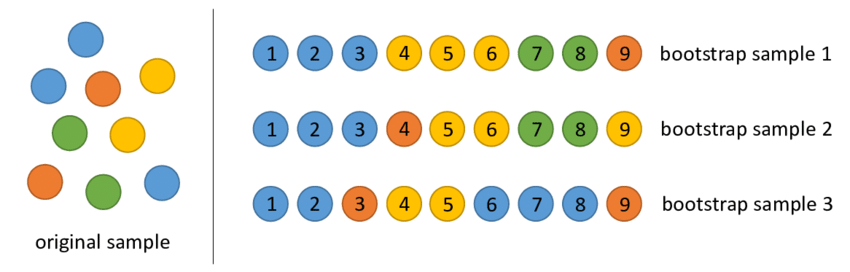
以下图为例：原始样本有9个，每个颜色代表一类，即原样本有4类（蓝色3个，绿色2个，橙色2个，黄色2个。采用bootstrap进行第一轮抽样，生成样本集合1：3个蓝球、3个黄球、2个绿球、1个橙球；接着进行第二轮抽样，生成样本集合2：3个蓝球、1个橙球、2个黄球、2个绿球、1个黄球。以此类推，重复该过程N次，得到N个新的数据集。

图片源自网络

二、Bootstrap方法的应用

统计学推断：在统计学中，bootstrap方法常用于推断总体的参数。举个简单的例子，通过bootstrap抽样，计算每个子样本的中位数，最终求其平均值，以得到总体中位数。
置信区间估计：与上述过程类似，在得到多个子样本的统计量（如均数、方差等）后，即可计算参数的95%置信区间。
预测模型验证：采用bootstrap进行抽样时，有一个特性，即总有一部分样本抽不到，比例大概为0.368。为此，利用该特性可以进行预测模型的验证。例如：（1）随机森林模型中，采用bootstrap方式进行决策树构建，而后进行集成，该模型就可以利用未采样数据（袋外数据）进行性能评价；（2）另一种通用方式是采用bootstrap对数据进行划分，即对于原始数据，采用bootstrap进行采样，将采样到数据用于模型训练，未采样到数据用于模型验证，且该过程可以执行多次，以获得置信区间等。