Python |
聚焦[MD]HVRP系列求解算法
之禁忌搜索算法
摘要
禁忌搜索算法+Split求解异构车辆路径规划问题

致力于打造交通领域优质代码分享平台

今天继续为大家分享 [MD]HVRP系列求解算法源码。欢迎:点赞+收藏+关注。后续将推送更多优质内容,为避免错过一个亿,建议星标。
异构车辆路径问题(heterogeneous fixed fleet vehicle routing problem,HVRP)是VRP的一类重要变体问题,相比于原始的VRP,进一步考虑了车辆的某些特性,比如装载量,行驶里程等。也有些研究是针对顾客的某些特性而言。这里的异构是指车辆的装载量存在差异,由此带来运输费用的差异。为了能够在多约束条件下寻求更好的求解效果,本期文章将复现经典文献中的改进Split算法,实现使其能够处理多(单)车场条件下考虑车辆装载特性的车辆路径规划问题。
01
注意事项
求解HVRP或MDHVRP
多车辆类型
车辆容量不小于需求节点最大需求
(多)车辆基地
车场车辆总数满足实际需求
02
实现思路
Christian Prins[2]给出的HVRP的Split方法过程如下:

以上算法在搜索过程中需求节点的备选标签规模会非常大,占用内存且降低搜索效率,因此采用了帕累托思想来遗传非支配解(19行~21行)。为了进一步控制备选标签数量,本期文章还附加实现了通过剩余容量与剩余需求来判断是否产生新的备选标签,提前避免产生不可行的标签。尽管如此,当考虑的异构车辆类型较多、需求点规模较大时,求解效率依然较低(代码结构、python特性、硬件环境)。所以本期文章进一步加入了最大标签数量参数来控制每个需求节点的备选标签规模,通过调节该参数实现速度与质量的相对均衡。
03
数据结构
继续以类的形式对算法参数、编码、解码、目标函数等进行封装。具体分为以下四类:
基本数据结构定义如下:
· Sol类:包含解的相关信息
| 属性 | 描述 |
|---|---|
| obj | 优化目标值 |
| node_id_list | 需求节点id有序排列集合 |
| route_list | 车辆路径集合 |
| action_id | 解所对应的算子id,用于禁用算子 |
·Demand类:包含需求节点的相关信息
| 属性 | 描述 |
|---|---|
| id | 物理节点id,需唯一。从0开始编号 |
| x_coord | 物理节点x坐标 |
| y_coord | 物理节点y坐标 |
| demand | 物理节点需求 |
·Vehicle类:包含车辆的相关信息
| 属性 | 描述 |
|---|---|
| depot_id | 所属车场id,不可与需求id重复 |
| capacity | 车辆装载率 |
| type | 车辆类型 |
| fixed_cost | 固定成本 |
| variable_cost | 单位里程变动成本 |
| numbers | 车辆数量 |
·Model类:包含全局参数
| 属性 | 描述 |
|---|---|
| sol_list |
种群集合,值类型为Sol() |
| best_sol | 全局最优解,值类型为Sol() |
| demand_dict | 需求节点集合(字典),值类型为Demand() |
| vehicle_dict | 车辆集合,值类型为Vehicle() |
| vehicle_type_list | 车辆类型集合 |
| demand_id_list | 需求id集合 |
| distance_matrix | 距离矩阵 |
| number_of_demands | 需求数量 |
| TL | 禁忌长度 |
| tau_list | 禁忌表 |
| max_labels | 最大备选标签数量 |
04
部分源码
参数读取

def readCSVFile(demand_file,depot_file,model):with open(demand_file,'r') as f:demand_reader=csv.DictReader(f)for row in demand_reader:demand = Demand()demand.id = int(row['id'])demand.x_coord = float(row['x_coord'])demand.y_coord = float(row['y_coord'])demand.demand = float(row['demand'])model.demand_dict[demand.id] = demandmodel.demand_id_list.append(demand.id)model.number_of_demands=len(model.demand_id_list)with open(depot_file, 'r') as f:depot_reader = csv.DictReader(f)for row in depot_reader:vehicle = Vehicle()vehicle.depot_id = row['depot_id']vehicle.x_coord = float(row['x_coord'])vehicle.y_coord = float(row['y_coord'])vehicle.type = row['vehicle_type']vehicle.capacity=float(row['vehicle_capacity'])vehicle.numbers=float(row['number_of_vehicle'])vehicle.fixed_cost=float(row['fixed_cost'])vehicle.variable_cost=float(row['variable_cost'])model.vehicle_dict[vehicle.type] = vehiclemodel.vehicle_type_list.append(vehicle.type)

def calDistanceMatrix(model):for i in range(len(model.demand_id_list)):from_node_id = model.demand_id_list[i]for j in range(i + 1, len(model.demand_id_list)):to_node_id = model.demand_id_list[j]dist = math.sqrt((model.demand_dict[from_node_id].x_coord - model.demand_dict[to_node_id].x_coord) ** 2+ (model.demand_dict[from_node_id].y_coord - model.demand_dict[to_node_id].y_coord) ** 2)model.distance_matrix[from_node_id, to_node_id] = int(dist)model.distance_matrix[to_node_id, from_node_id] = int(dist)for _, vehicle in model.vehicle_dict.items():dist = math.sqrt((model.demand_dict[from_node_id].x_coord - vehicle.x_coord) ** 2+ (model.demand_dict[from_node_id].y_coord - vehicle.y_coord) ** 2)model.distance_matrix[from_node_id, vehicle.type] = int(dist)model.distance_matrix[vehicle.type, from_node_id] = int(dist)

def calTravelCost(route_list,model):obj=0for route in route_list:vehicle=model.vehicle_dict[route[0]]distance=0fixed_cost=vehicle.fixed_costvariable_cost=vehicle.variable_costfor i in range(len(route) - 1):from_node = route[i]to_node = route[i + 1]distance += model.distance_matrix[from_node, to_node]obj += fixed_cost + distance * variable_costreturn obj
目标函数计算

def calObj(node_id_list,model):vehicle_routes = splitRoutes(node_id_list, model)if vehicle_routes:return calTravelCost(vehicle_routes,model),vehicle_routeselse:return 10**9,None
初始解

def generateInitialSol(node_id_list):node_id_list_=copy.deepcopy(node_id_list)random.seed(0)random.shuffle(node_id_list_)return node_id_list_
邻域算子

def createActions(n):action_list=[]nswap=n//2# 第一种算子(Swap):前半段与后半段对应位置一对一交换for i in range(nswap):action_list.append([1,i,i+nswap])# 第二中算子(DSwap):前半段与后半段对应位置二对二交换for i in range(0,nswap,2):action_list.append([2,i,i+nswap])# 第三种算子(Reverse):指定长度的序列反序for i in range(0,n,4):action_list.append([3,i,i+3])return action_list
提取路径

def extractRoutes(V,node_id_list,model):route_list = []min_obj=float('inf')pred_label_id=Nonev_type=None# search the min cost label of last node of the node_id_listfor label in V[model.number_of_demands-1]:if label[3]<=min_obj:min_obj=label[3]pred_label_id=label[1]v_type=label[2]# generate routes by pred_label_idroute=[node_id_list[-1]]indexs=list(range(0,model.number_of_demands))[::-1]start=1while pred_label_id!=1:for i in indexs[start:]:stop=Falsefor label in V[i]:if label[0]==pred_label_id:stop=Truepred_label_id=label[1]start=iv_type_=label[2]breakif not stop:route.insert(0,node_id_list[i])else:route.insert(0,v_type)route.append(v_type)route_list.append(route)route=[node_id_list[i]]v_type=v_type_route.insert(0,v_type)route.append(v_type)route_list.append(route)return route_list
05
代码结构
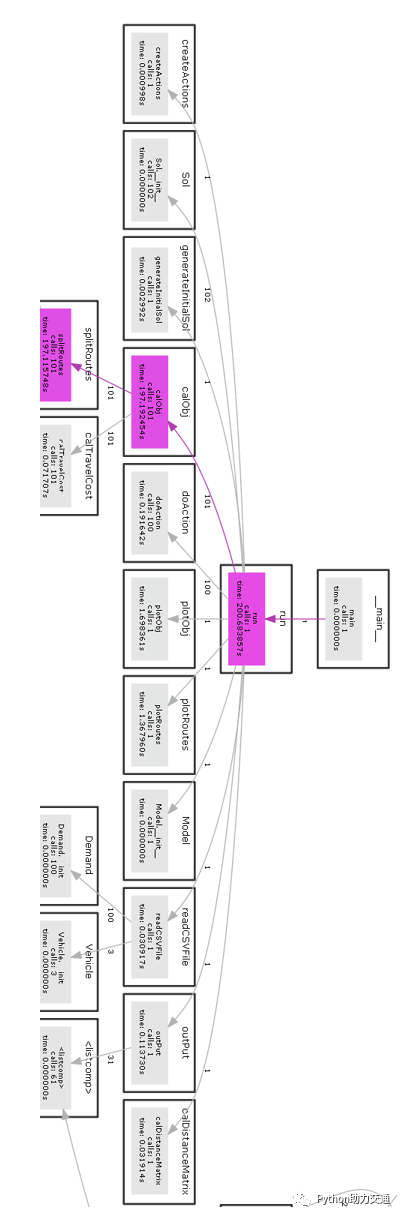
06
结果展示
这里采用solomon开源数据对算法进行测试,数据文件结构如下图所示,共100个需求点,3个车场,3类车辆,以.csv文件储存数据。
demand.csv文件内容如下图,其中第一行为标题栏,节点id从0开始递增编号。

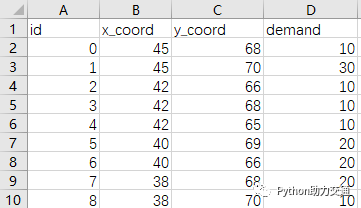

depot.csv文件内容如下图,其中第一行为标题栏,依次为:车场id,车场平面x坐标,车场平面y坐标,车辆类型,车辆装载量,车辆数量,固定成本,单位里程运输成本。

求解结果如下:
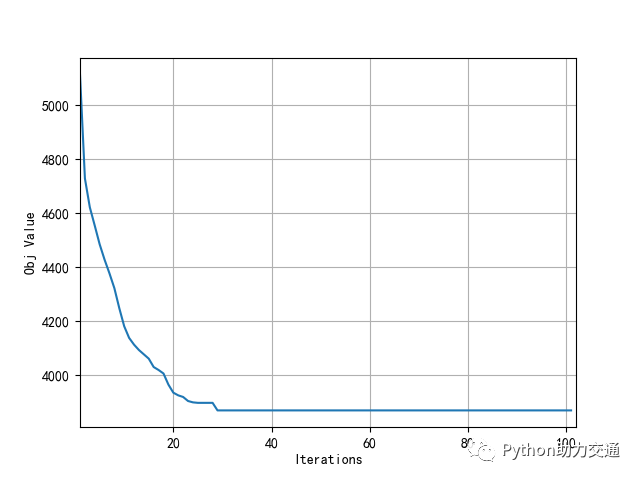
算法收敛图
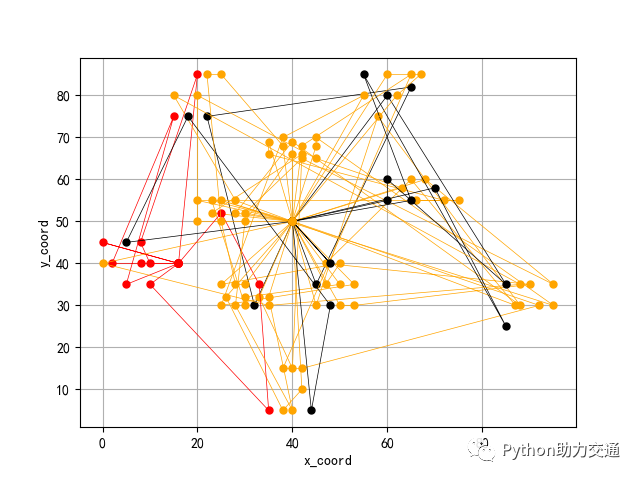
优化路线图
07
源码获取
①分享至朋友圈1小时以上
②凭分享截图后台回复 'TS_HVRP' 获取下载链接(链接有效期为30天)
08
参考
[1].汪定伟. 智能优化方法[M]. 高等教育出版社, 2007.
[2]Prins C , Lacomme P , Prodhon C . Order-first split-second methods for vehicle routing problems: A review[J]. Transportation Research Part C, 2014, 40(mar.):179-200.
扫码关注我们
欢迎点赞+收藏+关注

编辑 | 郭小安
校对 | 罩得住
点分享

点收藏

点点赞

点在看
文章评论