引言
变量之间相关性的直觉判定通常通过观察变量散点图来进行,数学判定由协方差公式来判断;变量之间相关性的程度由统计学三大相关系数来判定。在不同条件下,适用于不同的相关系数。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt#一次性导入需要的包
读取数据
math = [89,78,79,85,92,70,60]#math 成绩,生成一个list
physics = [92,63,76,88,90,73,62]#physics 成绩,生成一个list
grade = {'math':math,'physics':physics}#根据成绩,生成一个字典
data = pd.DataFrame(grade)#根据字典,生成一个dataframe,方便后面调用pandas的函数
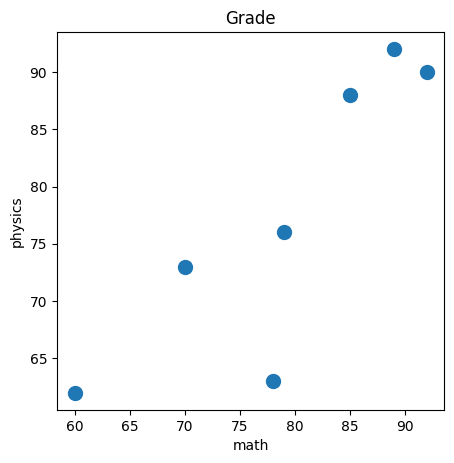
绘制散点图
plt.figure(figsize=(5, 5), dpi=100) #画布设置,可设置参数。画布可以不设置。
plt.scatter(math, physics,s=100) # 第一个参数为横轴。第二个参数为纵轴。 第三个参数为圆点大小,可选参数
#plt.scatter(math, physics,s=100,c='red',alpha=0.5) #红色圆点,半透明,scatter还有其他很多可选参数。感兴趣可以自行查阅官方文档或者相关资料进行学习
plt.xlabel('math')#横轴标签
plt.ylabel('physics')#纵轴标签
plt.title("Grade")#图题
plt.show()
协方差
#np.cov(math,physics)# 输出协方差矩阵
# np.cov(x,y)[0][0] #向量x的样本方差
# np.cov(x,y)[0][1] #向量x与y的协方差
# np.cov(x,y)[1][1] #向量y的样本方差
#data['math'].cov(data['physics'])#输出协方差值
data.cov()#输出协方差矩阵
| math | physics | |
|---|---|---|
| math | 124.666667 | 120.000000 |
| physics | 120.000000 | 158.238095 |
皮尔逊系数
data.corr()
#data.corr("pearson")#默认method 是"pearson",可以指定为“spearman”或者“kendall”
| math | physics | |
|---|---|---|
| math | 1.000000 | 0.854379 |
| physics | 0.854379 | 1.000000 |
斯皮尔曼系数
data.corr("spearman")
| math | physics | |
|---|---|---|
| math | 1.000000 | 0.928571 |
| physics | 0.928571 | 1.000000 |
从这里其实可以看到spearman系数对于异常值是有包容度的。计算得到的数值要比Pearson的值更大一些反映出来的数据相关性更强一些。
data.corr("kendall")
| math | physics | |
|---|---|---|
| math | 1.000000 | 0.809524 |
| physics | 0.809524 | 1.000000 |
文章评论