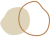
图7-49 是一条正态分布曲线,可以看出,曲线形似座钟,所以有时也被称作钟形曲线,特点是钟形两侧比较陡峭,到了尾部变得较平缓。
正态分布的均值和中位数是相等的,体现在图形上两个值所在的直线是完全重合的,并且这条直线正好处于正态分布曲线的波峰(曲线的最高点)。同时这条曲线只有一个波峰,因此也称为单峰曲线。正态分布曲线是完全对称的,如果沿着均值所在直线对折该图形,会得到完全重合的两个图形,其面积也是完全相等。
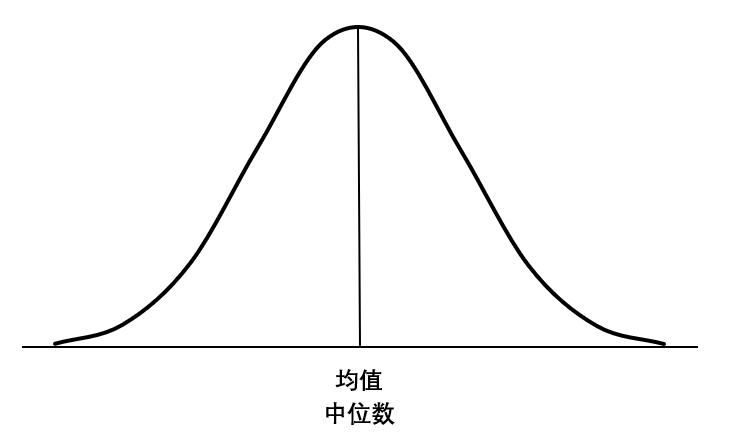
数据的两种趋势描述分别是集中趋势和离散趋势。正态分布中的集中趋势很明显,均值、中位数是重合的,其实正态分布的众数也是和均值重合的,读者可以自行验证。对于均值、中位数和众数完全相等的数据集,集中趋势就是其均值,它在曲线上的位置是恒定的,就是曲线的正中心。同样的,正态分布也有离散程度,能体现离散程度的标准差对曲线会产生怎样的影响呢,先看图 7-50 所示的不同标准差的正态分布曲线。
由图 7-50 可见,在均值相等的情况下,从均值向右挪动一个标准差后发现,标准差较大的分布离散程度大,表现在图上是曲线比较平缓;标准差较小的分布离散程度小,表现在图上是曲线比较陡峭。由此可见标准差对曲线形态影响之大。
因为正态分布的集中趋势只有一个值,所以当离散趋势的标准差确定以后,就可以完全确定整条曲线。
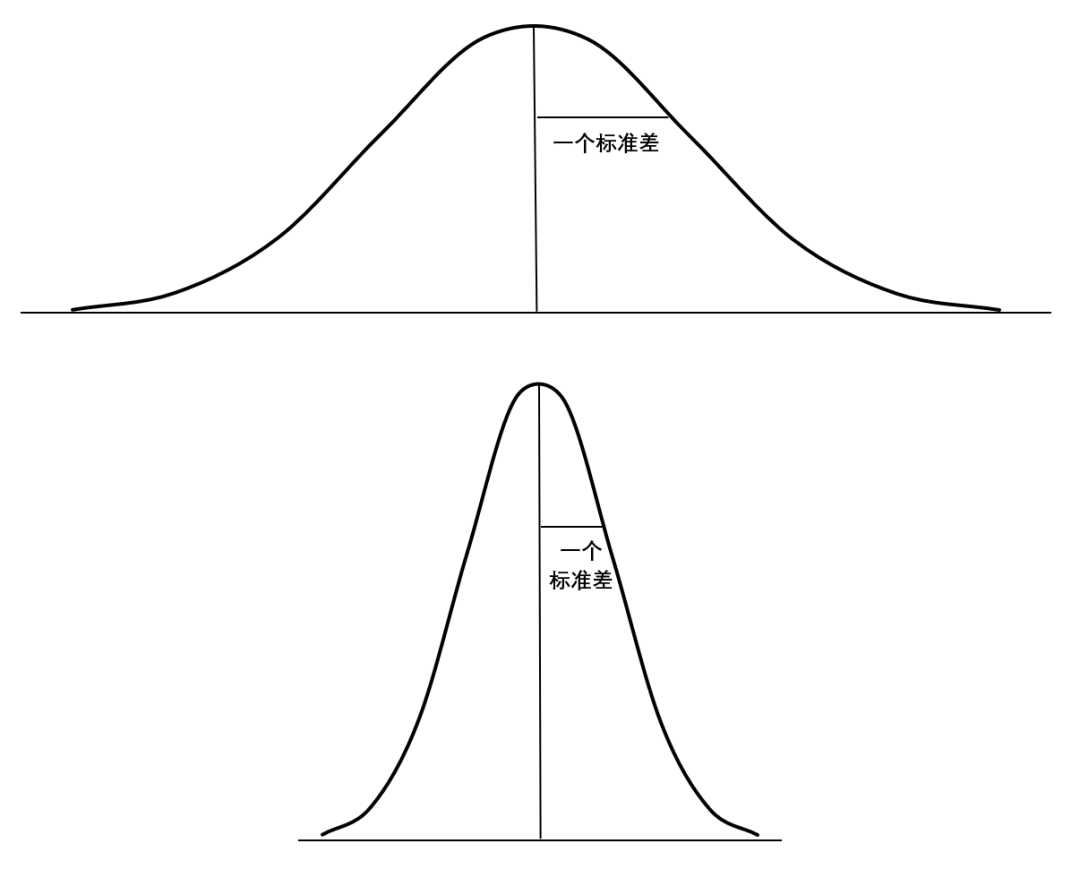
图7-51沿均值向两侧移动标准差
图7-51 是一组均值为 100,标准差为 10 的正态分布曲线。
图一是从均值出发,分别向两侧移动一个标准差的位置,即从 100 向左移动到 90 的位置,向右移动到 110 的位置,可以看到覆盖了图中的阴影面积,目测这部分面积已经超过整个钟形图面积的一半,统计学家已经给了答案,这部分的面积占比是 68.268949%,通常实际运算中直接取整为 68%(下面同理),因为正态分布曲线是完全对称的,那么以均值线为中心的两侧面积分别占比为 34%。
图二是从均值出发分别向两侧移动两个标准差的位置,分别到了 80 和 120 的位置,加上第一个标准差中的 68%,第二幅图的阴影面积已经达到 95%,同理,第三幅图 70 到 130 之间的阴影面积占比是 99.7%(非常接近 100%)。
移动 3 个标准差后的面积占比不会因为均值和标准差的变化而受到影响,任意的均值和任意的标准差组合出的曲线,都符合 68%、95%、99.7% 的占比,这就是 68-95-99.7 法则(也称为经验法则)。、
当一个正态分布的均值和标准差确定以后,就可以唯一确定这条曲线。有一条正态分布曲线比较特殊,是均值为 0,标准差为 1 的正态分布,它被称为标准正态分布,就是上一节中用来判断分布曲线峰度的标准线。
图 7-52 所示的 A1:A22 单元格区域是一组样本数据。现在需要制作其正态分布曲线,步骤如下。
步 骤 1计算出样本数据的均值和标准差。在 C2 单元格输入以下公式,得到样本均值是 62。
=AVERAGE(A2:A22)
在 C6 单元格输入以下公式,得到样本标准差是 8。
=STDEV.S(A2:A22)
注意:由于需要计算样本标准差,所以使用 STDEV.S,而不是 STDEV.P。具体请参阅 7.2.2 节内容。
结果如图 7-52 所示的 C1:D6 单元格区域所示。

步 骤 2将样本数据按组距为5的距离分组,分组坐标如图7-53所示的E2:E13单元格区域所示。
选择 F2:F13 单元格区域,在编辑栏输入以下数组公式,按< Ctrl+Shift+Enter>组合键。
=NORM.DIST(E2,$C$2,$C$6,FALSE)

步 骤 3选择 F1:F13 单元格区域,单击【插入】选项卡中的【插入折线图或面积图】→【折线图】命令,即可得到分组后的折线图,如图 7-54 所示。
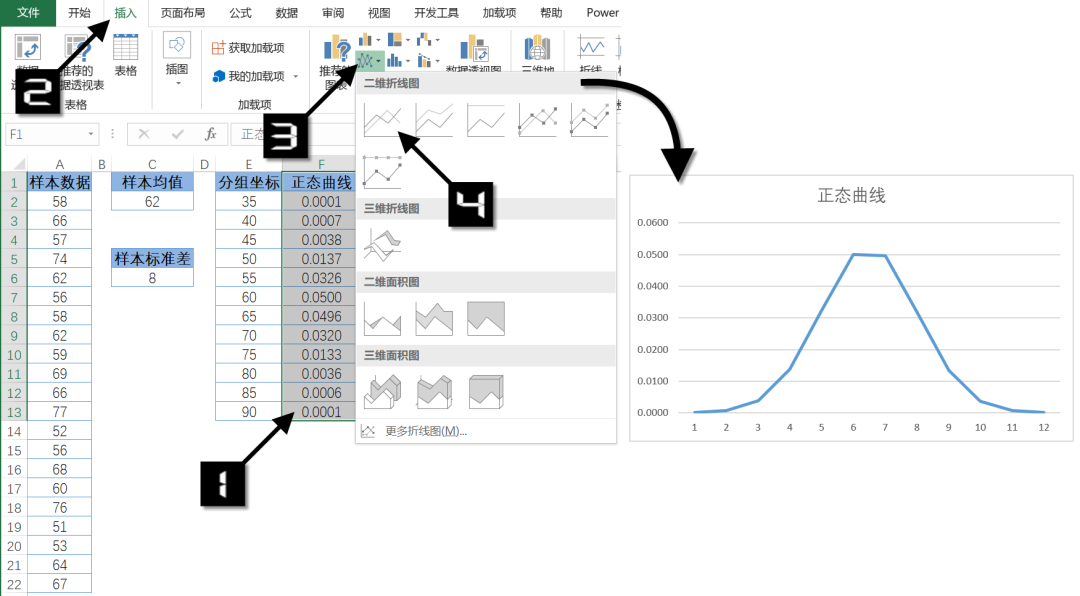
图7-54生成折线图
步 骤 4设置正确的坐标轴标签。选中图表,在【图表工具】的【设计】选项卡中单击【选择数据】按钮,打开【选择数据源】对话框。在【选择数据源】对话框中单击右侧“水平(分类)轴标签”的【编辑】按钮,打开【轴标签】对话框。设定轴标签区域为E2:E13,单击【确定】按钮关闭【轴标签】对话框,最后再次单击【确定】按钮关闭【选择数据源】对话框,即可将图标横坐标轴改为分组坐标,如图 7-55 所示。
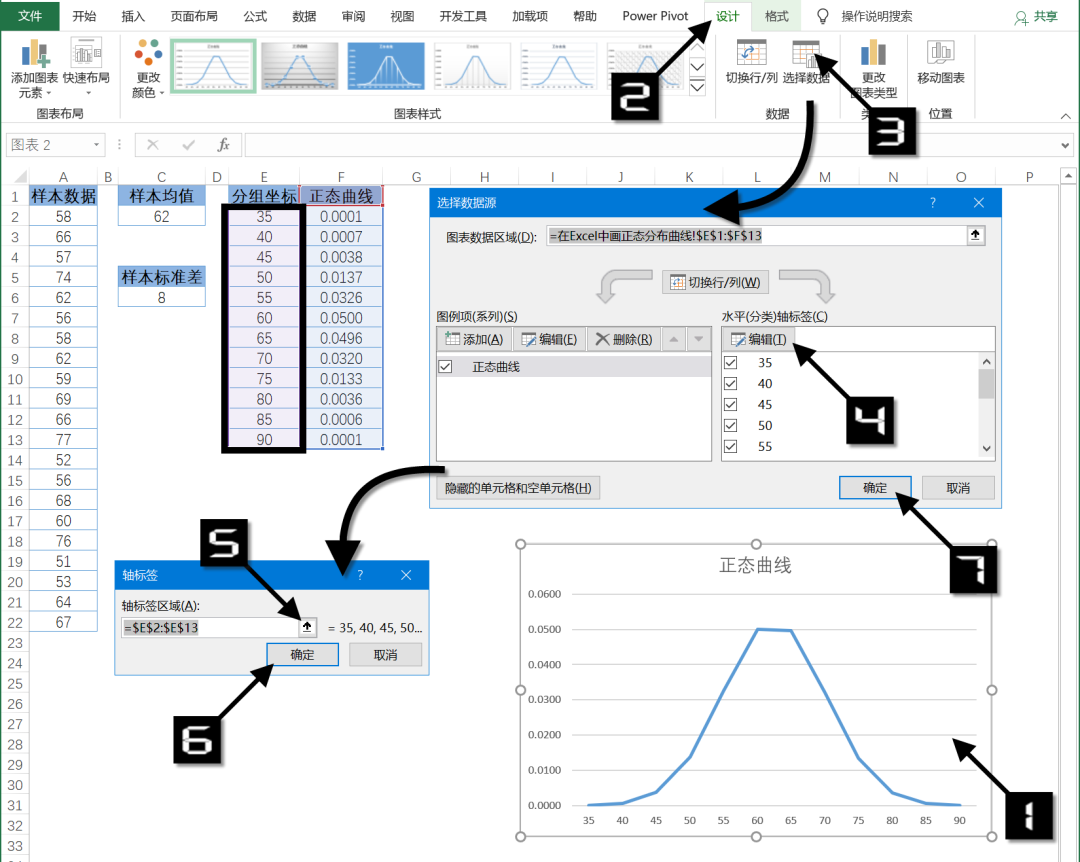
图7-55设置坐标轴标签
步 骤 5双击折线图中的折线,打开【设置数据系列格式】窗格。切换到【填充与线条】选项卡,选中【平滑线】复选框,即可得到平滑的正态分布曲线,如图 7-56 所示。
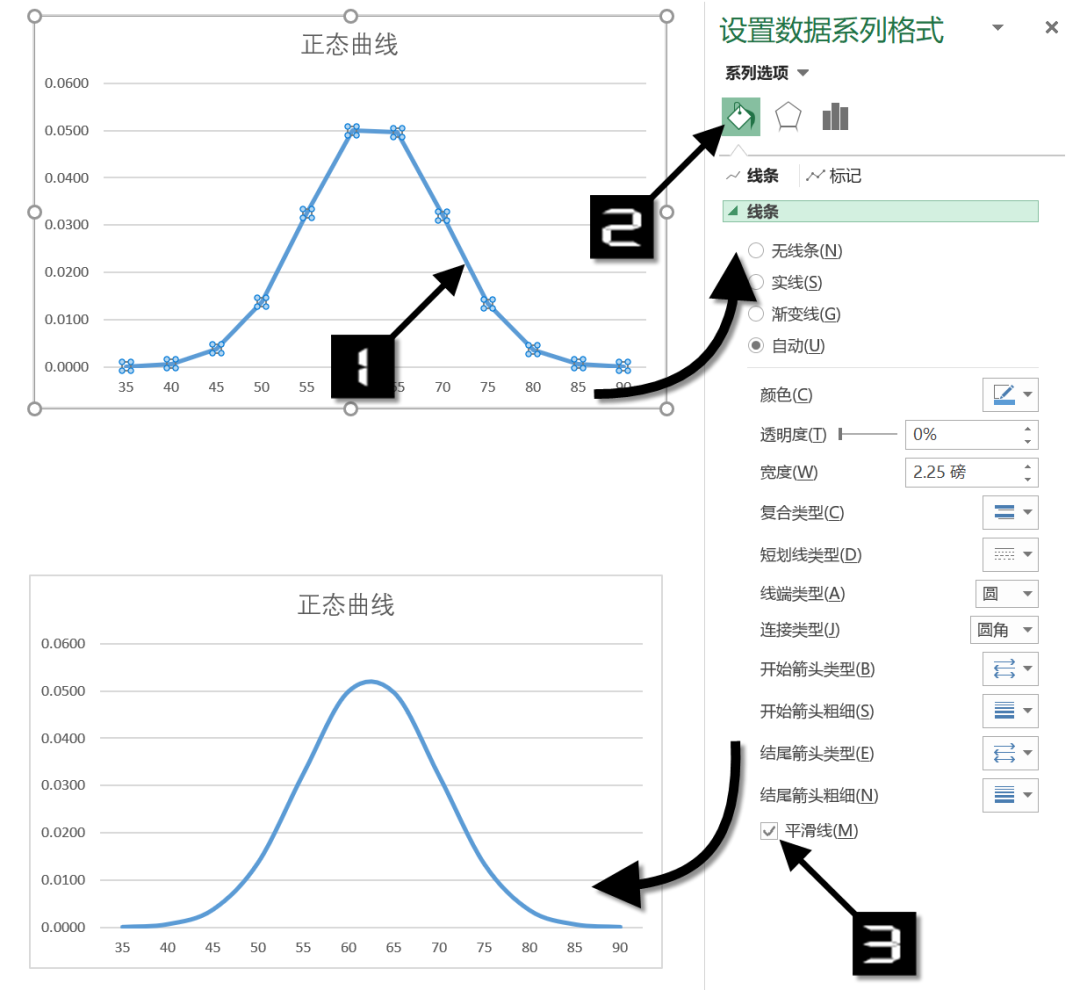
图7-56设置平滑曲线

假设 A 同学的身高是 170cm,想要知道这样的身高在班级中属于何种水平,就需要知道该班级全部学生的身高分布。现在已知该班学生的身高符合均值为 160,标准差为5 的正态分布,如图 7-57 所示。图中坐标轴上的圆圈标记出 A 同学的身高所在位置为 170,正好是沿均值向右移动两个标准差的位置,落在 170 左侧的阴影面积部分的同学身高都是低于 A 同学的。
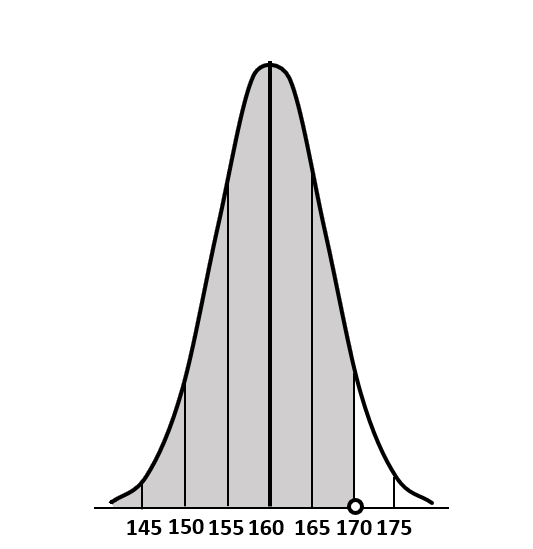
这部分阴影面积是多少呢,从均值 160 往左的全部面积(50%)+160 往右一个标准差面积(34%)+165 再往右一个标准差的面积(14%)=98%,所以 A 同学超过班上 98% 的学生身高,已经是顶尖的身高了。B 同学也来自该班,他的身高是 165,他的身高超过班里多少的学生呢,是 50%+34%=84%,所以 B 同学的身高超过了全班 84% 的同学。
根据上例得出结论,确定个体在总体里面的位置可以用标准差做度量单位。例如,C 同学比均值矮一个标准差,D 同学比均值高 0.5 个标准差。测量个体和均值之间相差了几个标准差就是标准值,也叫 z 值。计算方法如下。

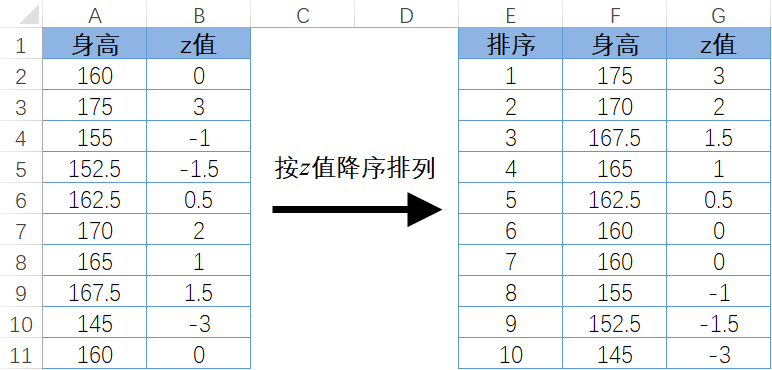
有了z值,可以很方便地测量每个数值在数据集中的位置。以 10 个同学的身高为例,求出每一个同学的 z 值,就可以用 z 值为同学们的身高排序,如图 7-58 所示。
如果 z 值是整数个标准差,很容易知道面积比例,如果不是整数,如 z 值为 1.27 要怎么判断呢,因为正态分布的各部分面积占比是不变的,所以统计学家早就做好了一张表,像查字典一样,根据 1.27 找到对应的面积占比即可。
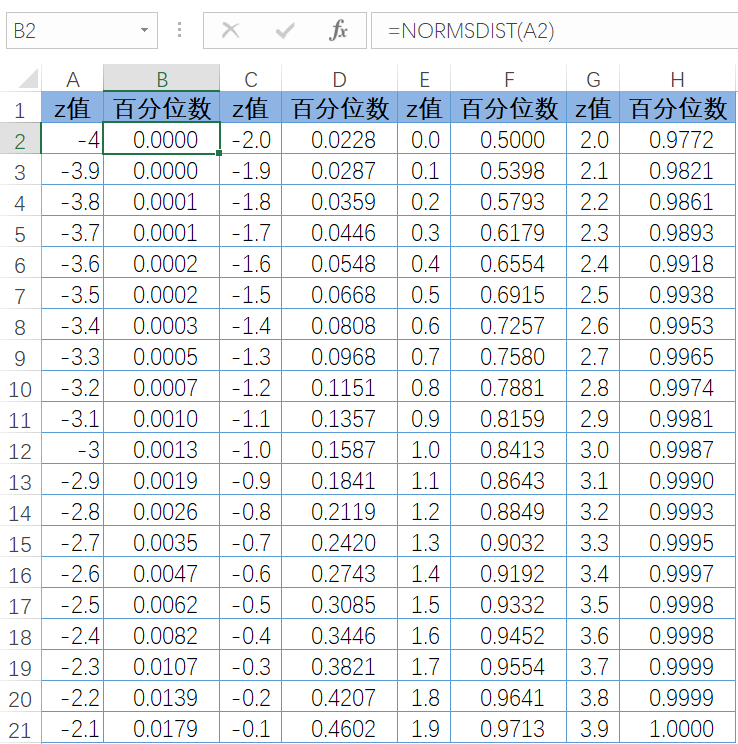
在计算机技术不发达的年代,z 值的百分位表都是统计学家做好,贴在统计学类书籍的附录中供读者查询,现在用 Excel 就可以自己制作百分位表,随时随地可以查询,步骤如下。
在 B2 单元格输入以下公式,并向下复制填充到 B3:B21 单元格区域。
=NORMSDIST(A2)
D 列、F 列和 H 列使用同样的方法设置公式,即可得到 z 值百分位数表,如图 7-59 所示。


推荐阅读
北京大学出版社
Excel数据处理与分析应用大全

文章评论