
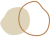
变量这个词,常出现在计算机、数学和统计等相关领域,在不同的环境中代表的意义也不同。例如,《全国人口普查条例》第十二条规定了普查内容:“人口普查主要调查人口和住户的基本情况,内容包括姓名、性别、年龄、民族、国籍、受教育程度、行业、职业、迁移流动、社会保障、婚姻、生育、死亡、住房情况等。”这些内容就是变量。
统计学不是研究个体的学科,而是研究总体的。例如,对于一个班级里的某一个学生,民族是确定的,但是对于全班总体而言,其中每一个学生的民族都可能不尽相同,民族这个变量会因为总体里面的个体不同而变化,这就是变量的特点。一个班里有 50 个学生,男生30 人,女生 20 人,如果对 30 个男生的身高做研究,那么身高这个变量就包含 30 个变量值,如果对 20 个女生的体重做研究,那么体重这个变量就包含 20 个变量值。
直方图是一组数据中所有数据的频次分布图,这组数据可以是一个班的学生体重,也可以是工厂出产的一批足球的直径,也可以是一个城市居民的收入,这个数据组也可以称为一个变量。集中趋势、离散趋势和正态分布等都可以用来描述变量,但都是针对一个变量进行描述。如果想研究两个变量之间关系,即一个变量发生变化时另一个变量会如何变化,就需要用到变量之间的相关关系。
例如,保险公司的精算师们经年累月地在研究什么因素会影响到寿命,什么因素会导致意外的发生,体重超过多少会引发疾病,车速多少会引起交通事故,等等。现在的人们上车第一件事就是系安全带,会在意外来临时保障安全,其实很多年以前人们没有这个意识,是保险公司通过大量的案例分析出来,系安全带后出交通事故比不系安全带的事故致死率要低很多。所以保险公司为了能少做理赔,最终推动了“上车一定要系安全带”这条法规的立法。
中国有句古话:有其父必有其子。虽然孩子的性格、外貌等特征并不全是由父亲决定的,也有母亲的因素,还有成长环境的影响,但是孩子和父亲的确有很大的关联。
最常用来展示两个变量之间关系的是散点图。散点图可以展示一组数据的两个变量之间的关系。散点图的做法很简单,某个同学的身高是 160cm,体重是 50kg,画在散点图上就是 X 轴 160 所在直线和 Y 轴 50 所在直线的交点。如果有多名同学,那么数据点也相应增多,如图 7-60 所示。
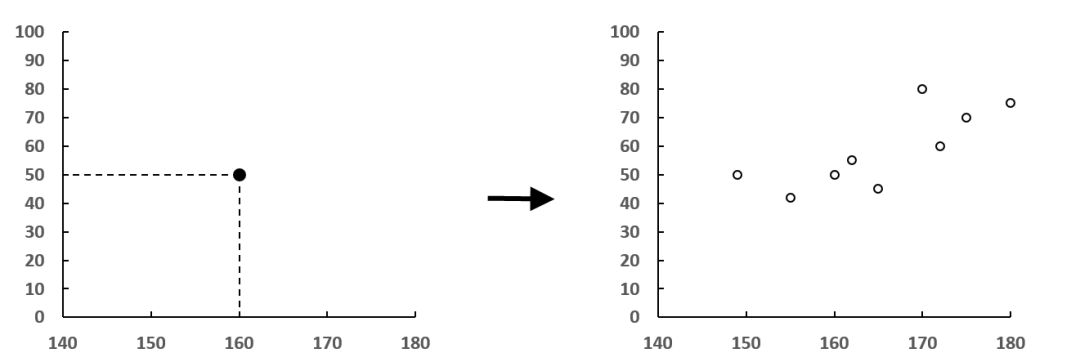
从散点图中可以直观看出变量之间的关系,如图 7-61 所示。如果所有点之间的关系可以近似地表现为一条直线,那么就称为数据线性相关。
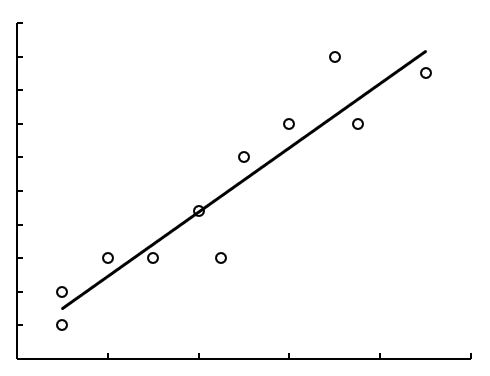
再观察图 7-62,也可以用直线近似表现所有点,但是这些点到直线的距离比较远,与图 7-61 相比是较弱的线性相关。
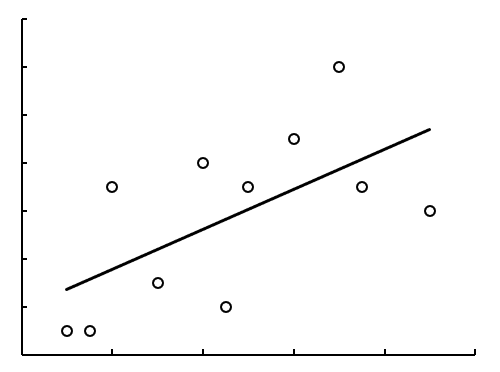
图7-62较弱的线性相关
如果散点图很松散,毫无规律,如图 7-63 所示,那么两个变量之间是完全不相关的。
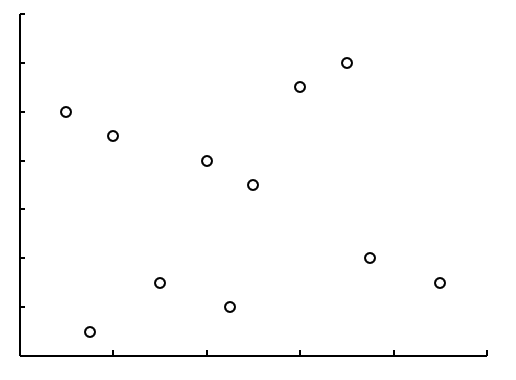
观察图 7-61 和图 7-62,无论相关的强弱关系如何,两条近似的直线都是从左下向右上方倾斜的,称为正相关,具体表现为一个变量数值增加,另一个变量的数值也增加。相反,如果直线是从左上向右下方倾斜,那么就是负相关,具体表现为一个变量的数值增加,另一个变量的数值减少,如图 7-64 所示。
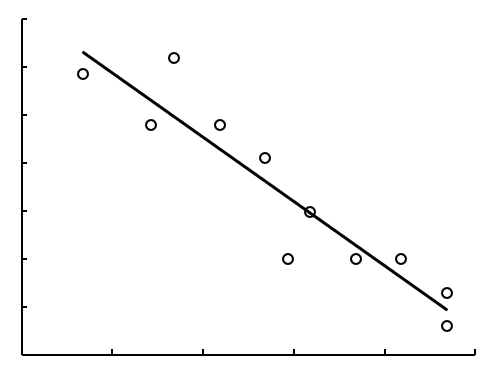
图7-64负相关

从散点图可以很容易地看出两个变量之间相关关系的正负方向和关系强度,当数据点分布很接近模拟线时,就是强相关;当数据点在线附近松散分布时,就是弱相关。仅凭肉眼只能观察到定性的内容,如果要知道强相关究竟有多强,弱相关究竟有多弱,就需要定量地分析,“相关系数”就是相关性的度量单位。
相关系数是对两个变量之间的相关关系的方向和强度的度量,通常用字符 r 表示,相关系数在任何统计软件中都会很容易得到。
从散点图的数据点分布是集中还是分散能看到两个变量的关系强弱,其实,这也是离散趋势的表现形式。离散趋势表现为一个横轴方向的离散,而散点图表现为横轴和纵轴两个方向同时离散,如图 7-65 所示。
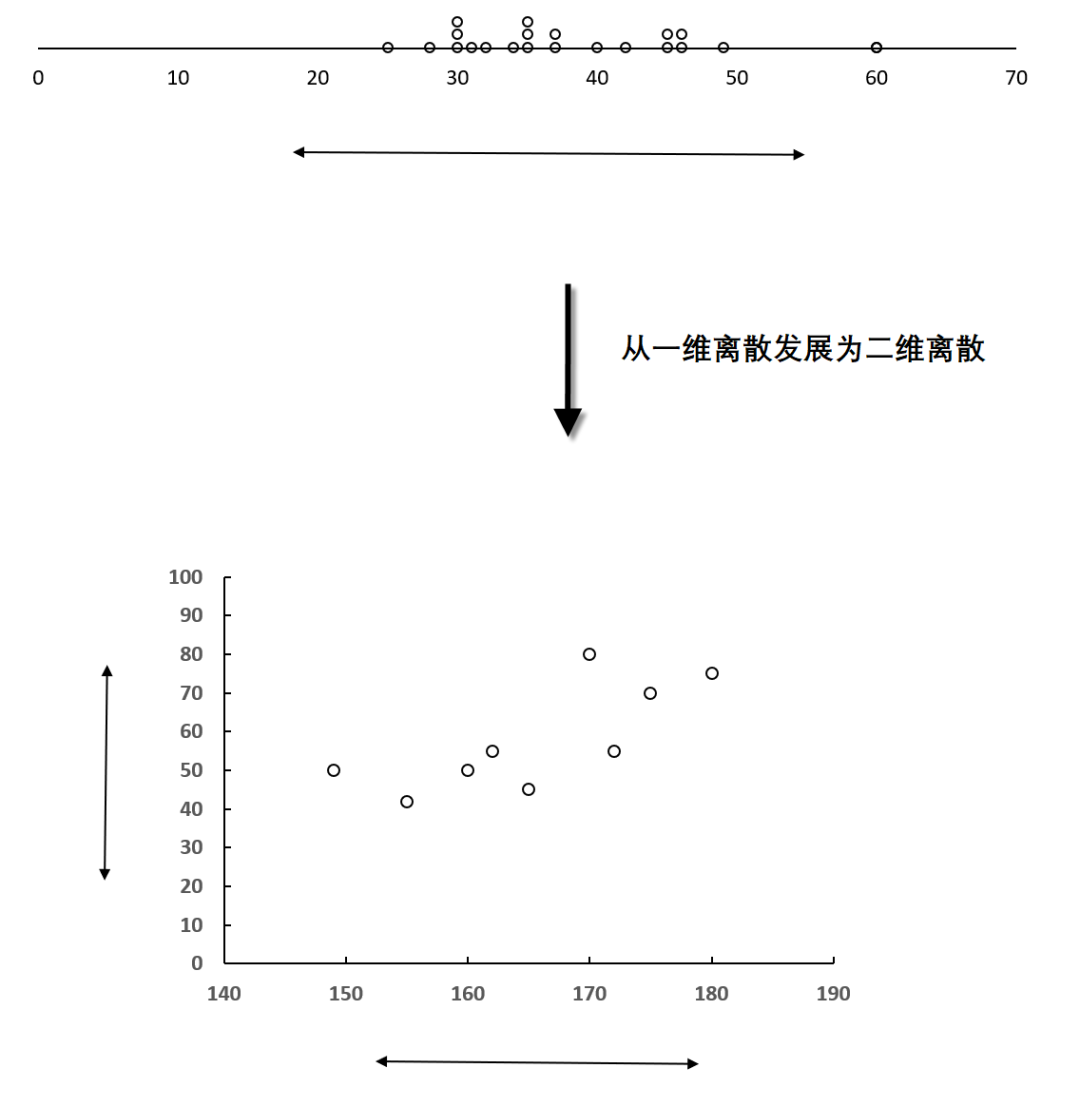
图7-65离散趋势从一维发展为二维
因此,可以用测量数据变动幅度的方法来研究相关关系,即从均值入手。
图 7-66 是 9 名学生身高体重的数据,变量为身高 X 和体重 Y。计算出身高的均值为165,体重的均值为 58。
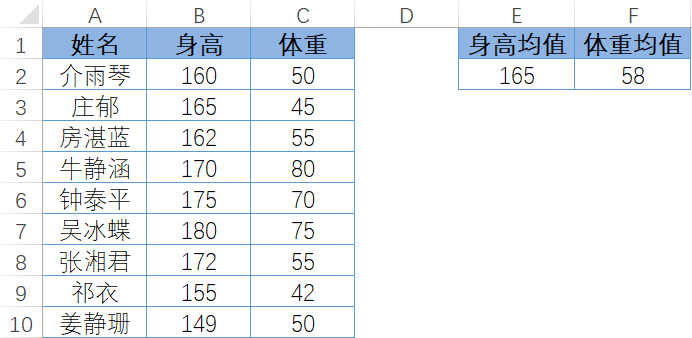
画出这组数据的散点图,用空心点表示,将均值点(165, 58)用实心点标出,如图7-67所示。
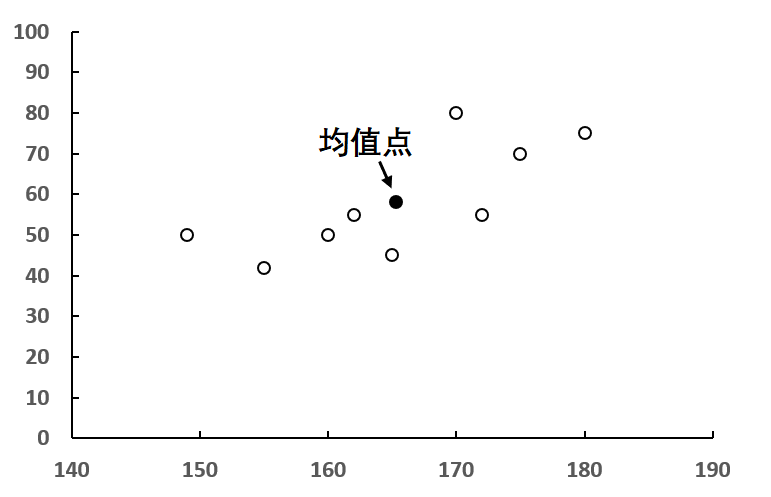
图7-67 9 个学生的身高体重散点图
注意:图 7-67 中的均值点并不是一个学生数据所在的点,而是根据身高均值和体重均值虚拟出来的,是相关系数计算中的重要参照点,可以将其想象为辅助线。每个点都与均值点有一定的距离,将这些距离加总就是整体偏离幅度。注意如何计算每个点与均值的距离呢?以第 5 行的牛静涵同学为例,牛同学身高为 170,体重为 80,相当于均值点在横轴方向往右移动了 5(170-165)的距离,记为 a ;同时在纵轴方向往上移动了 22(80-58)的距离,记为 b,如图 7-68 所示。
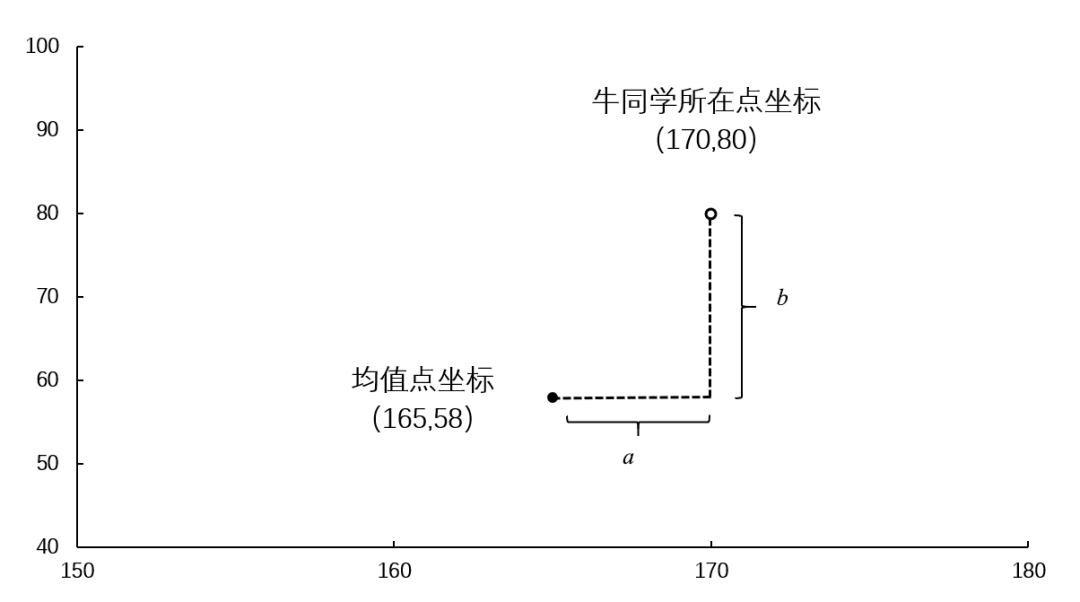
a 与 b 相乘就是牛同学所在点相对于均值点的变动幅度。
可是,体重与身高是不同单位不同数量级的数值,乘法运算对后续的分析比较起到了一定的副作用,如果要消除单位、数量级等因素的影响,可以使用标准值,即用 z 值衡量数值相对于均值移动了多少个标准差,用 z 值相乘即可(z 值的计算方法参见 7.4.4 节)。
如图 7-69 所示,牛同学的身高 z 值是 0.5,体重 z 值是 1.6,两个 z 值相乘 1.6×0.5=0.8,0.8 就是牛同学所在数据点相对于均值点的偏离程度。
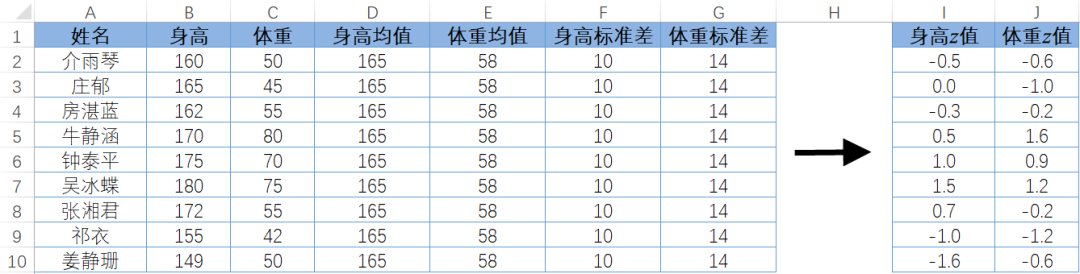
图7-69每个学生的身高 z 值和体重 z 值
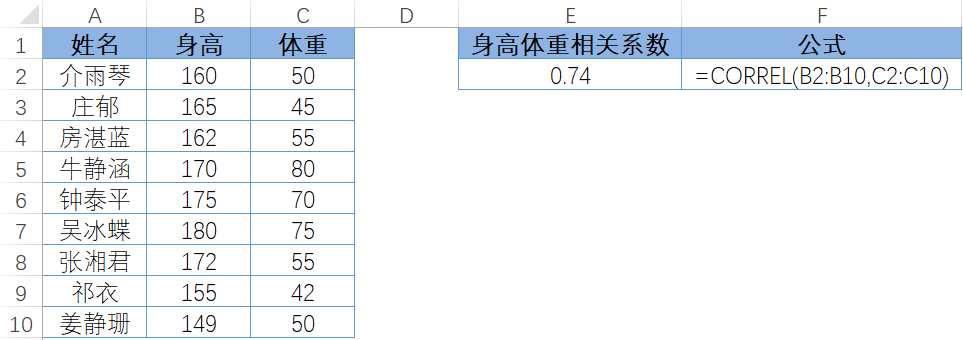
与此类似,先求出每个同学的偏离程度,然后由所有的偏离程度计算出均值就是相关系数。在本例中,相关系数是 0.74,求解过程如图 7-70 所示。注意,由于总体和样本的关系,在计算相关系数的均值时,不是除以 n,而是除以 n-1,计算标准差时也是用的 n-1,这是统计学中特殊的一点。
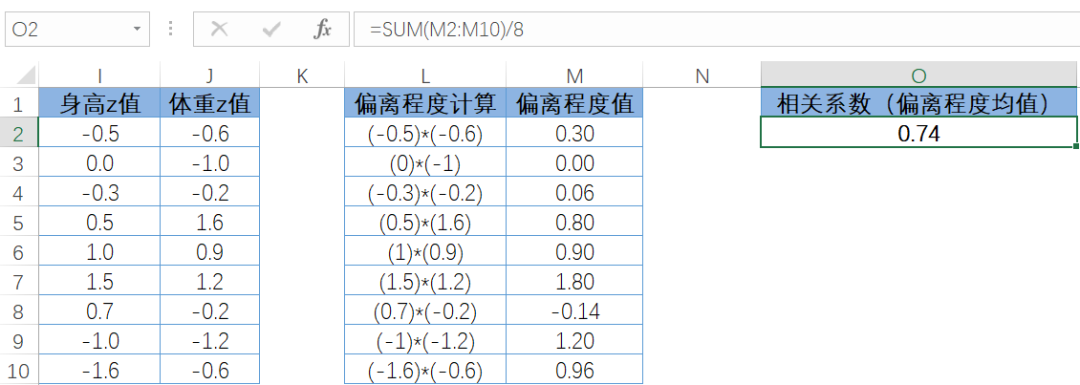
图7-70相关系数求解过程
把相关系数 r 用公式表示出来:
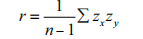
∑ 是代表后面的所有项求和, zx 是变量 X 的 z 值, z y 是变量 Y 的 z 值,这个公式表达的就是分别对两个变量的每一个数值计算 z 值,再将同一个数值的两个变量的 z 值相乘,最后将所有的 z 值乘积求得均值就是相关系数。
计算出相关系数以后,就要知道怎么应用它,如何度量相关关系呢?
第一,方向测量:r 如果是正数,说明两变量是正相关,r 如果是负数,说明两变量是负相关。
第二,强度测量:相关系数 r 是一个介于 -1 和 1 之间的数值。
也可以表示成
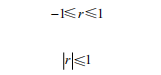
相关系数的绝对值越大,相关关系就越强;反之相关系数的绝对值越小,相关关系就越弱。通常统计学上对相关系数强度的细分如表 7-1 所示。
表 7-1 相关关系测量相关关系强弱
|
相关系数绝对值 |
相关关系强弱 |
|
0.8 ≤ |r| |
高度相关 |
|
0.5 ≤ |r| < 0.8 |
中度相关 |
|
0.3 ≤ |r| < 0.5 |
低度相关 |
|
|r| < 0.3 |
不相关 |
第三,相关系数具有对称性,它不会因为两个变量互换而变化。假设在图7-70的案例中,如果体重作为 X 变量,身高作为 Y 变量,最终得到的相关系数是不变的,依然是 0.74。第四,相关系数只对两个变量都是数值型才有意义。可以研究一个班级学生的出生地和民族的相关关系,但是无法用相关系数量化。


推荐阅读
北京大学出版社
Excel数据处理与分析应用大全


文章评论