题图 | 央视新闻 - https://weibo.com/u/2656274875
明天上午,谷爱凌将代表中国队冲击自由式滑雪女子U型场地技巧赛金牌。预祝她再创佳绩!

上图源自央视新闻微博
虽然谷爱凌获得大跳台首金已经过去好些天,但大家还意犹未尽地热议着她的“惊鸿一跳”。
碰巧我这段时间正在学图灵新出版的《程序员数学:用 Python 学透线性代数和微积分》一书,刚好学到用欧拉方法近似计算运动对象的轨迹。
谷爱凌的凌空一跃让我灵光乍现:这不就是绝佳的练手机会吗?
所谓学以致用,我决定尝试用书中知识模拟谷爱凌的大跳台抛物线。
更具体的背景知识请见《程序员数学:用Python学透线性代数和微积分》一书的第 9 章。
接下来就开始吧!
我们要做的是编写一个 Python 函数,用来实现欧拉方法,然后用该函数模拟谷爱凌的致胜一跳。
欧拉方法是一种近似积分的重要技巧。它的核心思想是从一个量的初始值(如坐标)和一个描述其导数(如速度和加速度)的方程开始,根据导数求这个量变化后的值。
定义“爱凌跳”函数
我把这个Python 函数命名为eileen_jump。它接受以下参数。
- s0:初始坐标
- v0:初始速度
- a:加速度向量
- total_time:要模拟的总时间
- step_count:步数
以下是函数 eileen_jump 的定义,其中的函数 add 和 scale 稍后定义。
def eileen_jump(s0,v0,a,total_time,step_count):trajectory = [s0]s = s0v = v0dt = total_time/step_count # 每个时间阶段的持续时间dt是总时间除以步数for _ in range(0,step_count):s = add(s,scale(dt,v))v = add(v,scale(dt,a))trajectory.append(s)return trajectory
计算参数值
当谷爱凌从首钢滑雪大跳台腾空时,她的重力加速度是 9.80 m/s²。重力加速度是一个指向地心的向量,任何抛射物(人)都有同样的加速度向量。
我们以大跳台为基础,构建一个二维坐标系。在这个坐标系中,谷爱凌腾空时刻的加速度向量为:
a = (0, -9.80)
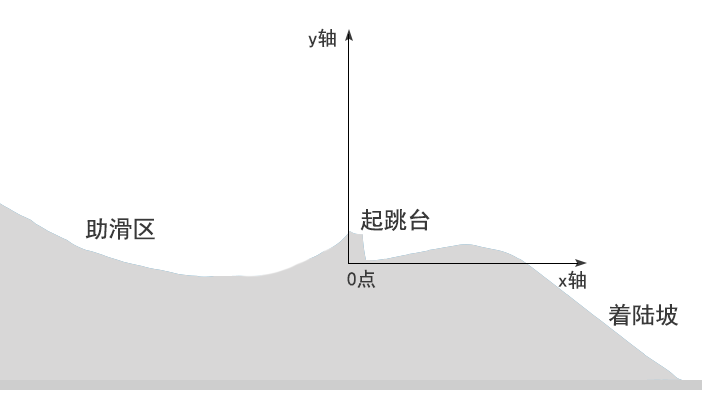
根据清华大学建筑学院院长、首钢滑雪大跳台总设计师张利在《开讲啦》分享的一张设计图,我粗略计算,首钢滑雪大跳台的起跳台高度约为 4 米。
也就是说,谷爱凌腾空时刻的坐标为:
s0 = (0, 4)
根据媒体发布的数据,谷爱凌的起跳角度约为 35 度,起跳速度约为 13.8m/s,因此初始速度为:
(13.8·cos(35°), 13.8*sin(35°))
剩下两个参数可以这样取值。
total_time = 2.3
step_count = 100
模拟轨迹
万事俱备,接下来导入要用到的 Python 包,开始模拟。完整代码如下所示:
from math import pi,sin,cosimport matplotlib.pyplot as plt# 定义scale函数def scale(scalar,v):return (scalar * v[0], scalar * v[1])# 定义add函数def add(v1,v2):return (v1[0] + v2[0], v1[1] + v2[1])# 定义eileen_jump函数def eileen_jump(s0,v0,a,total_time,step_count):trajectory = [s0]s = s0v = v0dt = total_time/step_count # 每个时间阶段的持续时间dt是总时间除以步数for _ in range(0,step_count):s = add(s,scale(dt,v))v = add(v,scale(dt,a))trajectory.append(s)return trajectoryif __name__ == '__main__':angle = 35 * pi/180s0 = (0,4)v0 = (13.8*cos(angle),13.8*sin(angle))a = (0,-9.80)result = eileen_jump(s0,v0,a,2.3,100)for r in result:x, y = r[0] , r[1]plt.scatter(x,y)plt.show()
模拟结果如下:
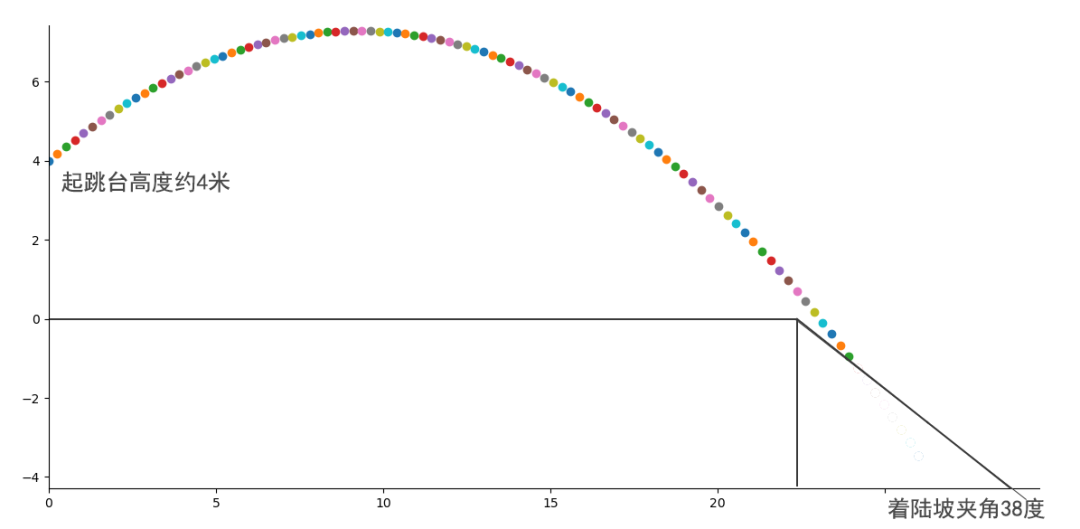
当然,各个参数的取值并不严格精确。如果能知道它们的精确值,那么模拟结果将更准确。
新 书 推 荐

保罗·奥兰德(Paul Orland)——著
百度KFive —— 译
代码和数学是相知相惜的好伙伴,它们基于共同的理性思维,数学公式的推导可以自然地在编写代码的过程中展开。
本书将带领程序员使用自己擅长的工具,即代码,来解决机器学习和游戏设计等领域中的数学问题,重新发现数学之美。


名人推荐
“这本书循序渐进地介绍了程序员应该掌握的有用的数学概念。”
——Christopher Haupt,Swoogo 公司工程副总裁
“这本书严谨而简明地概述了对现代编程起支撑作用的数学知识。”
——Dan Sheikh,BCG Digital Ventures 公司工程师
“实用、引人入胜。推荐所有程序员阅读。”
——Vincent Zhu,RethinkXSocia 网站联合创始人兼CTO
“这本书为需要提高数学技能的程序员建造了一座桥梁,使数学不再那么神秘、那么难以理解。”
——Robert Walsh,Excalibur Solutions 公司总裁

参考资料:
https://tv.cctv.com/2021/10/24/VIDEd6UZkFcseVOReA7Wvpqw211024.shtml
https://content-static.cctvnews.cctv.com/snow-book/video.html?item_id=17236332578558502720
https://w.yangshipin.cn/video?type=0&vid=f000010uqrc&channel=ysyy_aoyun
各位小伙伴,如果您对这本书感兴趣可以加下面的群,在这里你会找到更多志同道合的小伙伴,可以一起探讨一下学习python或数学时面临的问题~
python交流群

数学交流群

文章评论