爬虫工程师如何绕过验证码？寻找阿登高地之路

2017年7月19日 342点热度 0人点赞 0条评论

导读：马奇诺防线是二战前法国耗时十余年修建的防御工事，十分坚固，但是由于造价昂贵，仅修建了法德边境部分，绵延数百公里，而法比边界的阿登高地地形崎岖，不易运动作战，且比利时反对在该边界修建防线，固法军再次并没过多防备，满心期望能够依靠坚固的马奇诺防线来阻挡德军的攻势。没想到后来德军避开德法边境正面，通过阿登高地从防线左翼迂回，绕过了马奇诺防线，然后就是英法联军的敦克尔克大撤退了。

网站验证码就如同马奇诺防线一样，阻挡了爬虫工程师的正面进攻。

随着爬虫和反爬虫双方围绕验证码的不断较量，最终导致了验证码识别难度的不断上升。现在复杂的验证码长这样：

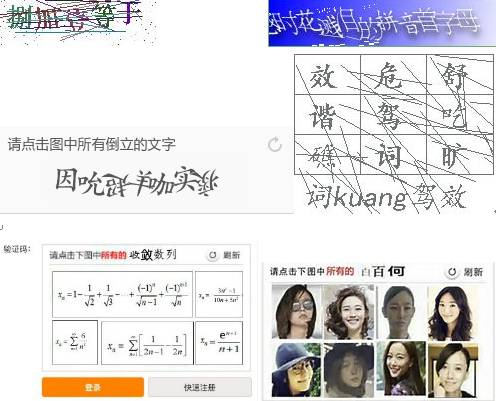
正面硬刚验证码，想要识别它，是件挺复杂的事，涉及到图像处理技术：二值化，降噪，切割，字符识别算法：KNN(K 邻近算法)和 SVM (支持向量机算法)，再复杂点还要借助 CNN(卷积神经网络)，还有什么机器学习啥的。

虽然现在有打码平台可以解决绝大多数的验证码问题，但如果爬取的数量特别庞大，单纯依赖打码平台也是不大行得通的，除了成本因素，还有打码平台也解决不了的验证码因素，比如滑动验证码：

既然正面进攻费事费力，那能不能找到爬虫工程师眼中的阿登高地绕过验证码？

本文以各地工商网站为例，对常见的验证码绕过技巧做一个小总结，顺便解密下如何不借助模拟 js 拖动来绕过滑动验证码。

各地工商网站（全称国家企业信用信息公示系统）因为包含大量企业真实信息，金融贷款征信等都用得到，天然吸引了很大部分来自爬虫的火力，因此反爬虫措施格外严格。一般的网站仅在登录注册等环节，或者访问频繁后才弹出验证码，而工商网站查询无需登录，每查一次关键字就需要一次验证码。同时各地工商网站由于各自独立开发，自主采用了各种不同的验证码机制，更是给全量爬取的爬虫增加了更多的障碍。因此，工商网站的验证码特别具有代表性。

首先，从最简单的分页角度入手。

分页的处理可以放在前端也可以放在后端，如果只放在后端，每次点击页码就需要发送一次查询请求，而一次验证码通常只能服务于一次请求，再次请求需要获取新的验证码，直接观察翻页操作是否弹出验证码输入框即可判断是否可以绕过。

如何判断分页处理放在前端还是后端的呢？很简单，F12 打开浏览器开发者工具，页面点下一页，有新的请求就说明放在后端，反之就是前端。

实践发现，四川和上海的工商网站翻页都放在后端，且翻页没有验证码输入框。说明这里的验证码可以绕过，但是绕过的原理却有些不同：

对比四川工商网站翻页前后请求的参数，除了页码参数外，多了一项：yzmYesOrNo=no。从变量名也猜得到，后端根据该参数的值判断是否需要检查验证码。
而上海工商网站的对比结果发现，除了页码参数外，少了验证码字段，因此我们可以大胆猜测：验证码的校验仅放在了前端，后端没有做二次校验，从页面上操作是绕不过的，但是不带验证码字段直接向后端发送请求，数据就拿到了。

严格来说，上海工商网站这种算是漏洞，对待这种这种漏洞，爬虫工程师应有的态度是：悄悄的进村，打枪的不要。不过也不要利用的太狠了，笔者实验时没加限制，爬了十万数据后，ip 被封了。很长时间后才解封，同时页面改版并修复了漏洞。

其次，观察目标网站是否有多套验证码。

有些网站不知道出于什么样的考虑，会在不同的页面使用不同的验证码。一旦遇到这种情况，我们可就要捡软柿子捏了--从简单的验证码入手，移花接木，将识别的结果作为参数来向后端发送请求，从而达到绕过复杂验证码的目的。

举例来说，湖北工商的查询页面验证码是类似下图的九宫格验证码：

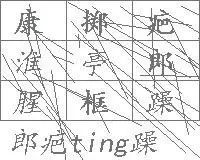
而电子营业执照登陆界面的验证码是这样的：

即便要识别，也明显是后者的验证码要容易些，实例代码如下：

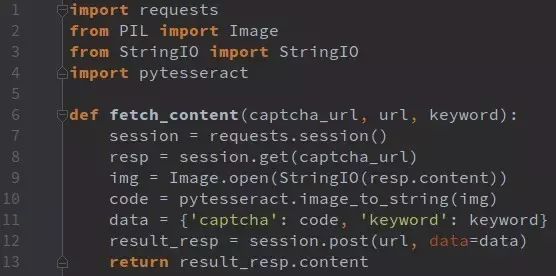
再者，可以考虑从数据的存储id入手

专门针对移动端开发的 wap 页面限制一般要少得多。以北京工商网站来说，wap 界面不带验证码参数直接发送请求就可以得到数据的，原理类似于上海工商网站，但是其对单个ip日访问次数做了严格限制，因此该方式可以用但不好用。

继续观察，以搜索“山水集团”为例，从搜索页到列表页时，需要输入验证码，而从列表页进入详情页的时候，是不需要验证码的。最终详情页如图：

通常没人记得住各地工商网站的网址，我们会去搜索引擎里搜。当搜北京企业信用信息时，发现两个有价值的结果，除了国家企业信用信息公示系统外，还有个北京市企业信用信息信息网。进后者再操作一番可以得到下面的详情页：

观察发现，企业 id 都是相同的，嘿嘿，这不是“两块牌子，一套班子”嘛！后者的访问量要小一些，虽有验证码，但是可以采用上海工商一样的方式绕过，只是返回的结果字段不太符合我们的要求。不过，我们可以去企业信息网获得企业id，再次采用移花接木的方式，去信息公示系统构造链接获得最终的详情页嘛！

用过数据库同学都晓得，数据库里的数据 id，默认是自增的。如果有个网站引用的数据是 xxx.com?id=1234567, 那我们很容易猜得到构造类似 1234568 这样的 id 去尝试！通常，使用这种 id 规律能够轻易猜出来的网站并不多，但不代表没有。比如甘肃省工商网站，结果页是拿企业注册号来查询的。

最后，谈谈滑动验证码。

目前，工商网站已经全面改版，全部采用了滑动验证码，上面绝大多数思路都失效了。对于滑动验证码，网上能搜到的解决方案基本都是下载图片，还原图片，算出滑动距离，然后模拟 js 来进行拖动解决，我们来看下能否不模拟拖动来解决这个问题。

以云南工商网站为例，首先抓包看过程。

1. http://yn.gsxt.gov.cn/notice/pc-geetest/register?t=147991678609，response：

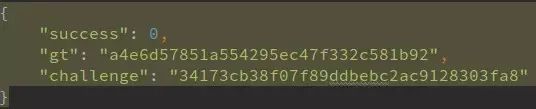
2. 下载验证码图片

3. http://yn.gsxt.gov.cn/notice/pc-geetest/validate， post 如下数据：

4. http://yn.gsxt.gov.cn/notice/search/ent_info_list，post 如下数据：

仔细分析，我们发现两处疑点：

第一步并没有返回需要下载的图片地址，那么前端怎么知道要下载哪些图片？
第三步验证时，并没有告知后端下载了那些图片，后端是怎么验证 post 过去的数据是有效性的？

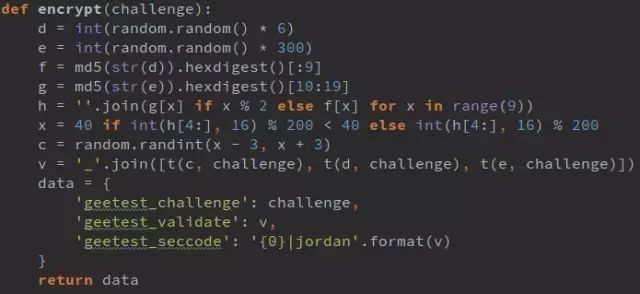
仔细阅读前端混淆的 js 代码，我们发现前端数据处理过程是这样的：

从 0 到 6（不含）中取随机整数，赋值给 d， d=5；
从 0 到 300（不含）中取随机整数，赋值给 e， e=293；
将d转化为字符串并作 MD5 加密，加密字符串取前 9 位赋值给 f， f='e4da3b7fb'；
将 e 转化为字符串并作 MD5 加密，加密字符串从第 11 位开始取 9 位赋值给 g, g='43be4f209'；
取 f 的偶数位和 g 的奇数位组成新的 9 位字符串给 h, h='e3de3f70b'；
取 h 的后 4 位与 200 做 MOD 运算，其结果小于 40，则取 40，否则取其本身赋值给 x，x=51；
取 [x-3, x+3] 以内随机数赋值给 c，c=51；
分别取 c,d,e 跟 challenge 做 t 加密 (t(c,challenge), t(d, challenge), t(e,challenge)) 并用（_）拼接即为 geetest_validate, '9ccccc997288_999c9ccaa83_999cc9c9999990d'
这里 f, g 参数决定了下载图片地址：

而 x 为滑块拖动的横向偏移量，至此解答了疑问 1 中图片下载地址怎么来的问题。

前边提到的 t 加密过程是这样的：

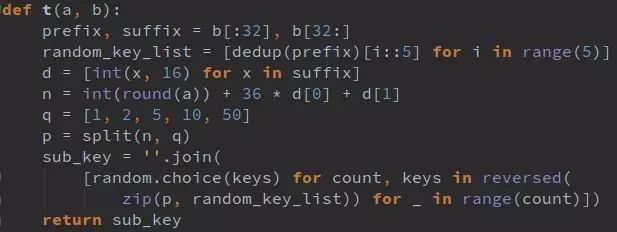
t(a,b)，此处以 a=51 演示

challenge 为 34 位 16 进制字符串，取前 32 位赋值给 prefix，后 2 位赋值给 suffix，prefix='34173cb38f07f89ddbebc2ac9128303f', suffix='a8'
prefix 去重并保持原顺序，得到列表 ['3', '4', '1', '7', 'c', 'b', '8', 'f', '0', '9', 'd', 'e', '2', 'a']
将 2 中列表循环顺序放入包含 5 个子列表的列表中，得到random_key_list： [['3', 'b', 'd'], ['4', '8', 'e'], ['1', 'f', '2'], ['7', '0', 'a'], ['c', '9']]
将 suffix 字符串（16 进制）逐位转化为 10 进制，得到 [10, 8]
将 4 中列表逐位与 [36,0] 做乘法和运算并与 a 的四舍五入结果相加， n= 51 + 36*10 + 0*8=419
q=[1,2,5,10,50], 用 q 对 n 做分解（n=50*13+10*0+5*1+2*1+1*1），将其因数倒序赋值给 p，p=[0,2,1,1,8]
从 random_key_list 右侧开始随机取值，次数为 p 中数值，拼成字符串 sub_key，sub_key='9ccccc997288'

至此，我们完成了整个分析过程，我们又有了新发现：

按照前边的抓包过程，其实不需要真的下载图片，只需执行 1、3、4 步就可以得到目标数据了。步骤 1 也可以不要，只需 3、4 即可，但是少了步骤 1，我们还需要额外请求一次 cookie，所以还是保留 1, 这样也伪装的像一点嘛。
相同的 challenge，每次运算都可以得出不同的 validate 和 seccode，那么问题来了：到底服务端是怎么根据 challenge 验证其他数据是否有效呢？

总结一下，对于验证码，本文只是提供了一种新的思路，利用了网站开发过程中的一点小疏漏，而最后的滑动验证码也只是分析了 offline 模式的验证方法。不要指望所有验证码都可以能绕过，没有阿登高地，二战德国就不打法国了么？只要觉得有价值，即使正面面对验证码，作为爬虫工程师建议也就一句话：不要怂，就是干！

推荐阅读